非线性声学

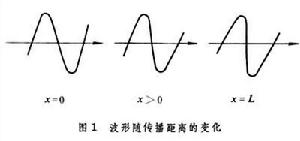
非线性声学 (NLA) 是物理学和声学的一个分支，处理足够大振幅的声波。 大振幅需要使用完整的流体动力学（液体和气体中的声波）和弹性（固体中的声波）控制方程组。 这些方程通常是非线性的，它们的传统线性化不再可能。 这些方程的解表明，由于非线性效应，声波在传播时会发生扭曲。

声波作为局部压力变化通过材料传播。 增加气体或流体的压力会增加其局部温度。 可压缩材料中的局部声速随温度升高而增加； 结果，波在振荡的高压阶段比在低压阶段传播得更快。 这会影响波的频率结构； 例如，在单一频率的初始纯正弦波中，波峰比波谷传播得更快，并且脉冲累积起来更像锯齿波。 换句话说，波会扭曲自身。 在这样做的过程中，引入了其他频率分量，可以用傅里叶级数来描述。 这种现象是非线性系统的特征，因为线性声学系统仅响应驱动频率。 这种情况总是会发生，但几何扩散和吸收的影响通常会克服自失真，因此线性行为通常占主导地位，而非线性声学传播仅在非常大的振幅且仅在声源附近发生。

此外，不同振幅的波将产生不同的压力梯度，从而导致非线性效应。

介质内的压力变化导致波能转移到高次谐波。 由于衰减通常随频率增加，因此存在一种反作用，它会改变非线性效应随距离的性质。 为了描述它们的非线性水平，可以给材料一个非线性参数 B / A 。值是材料压力与其密度相关的泰勒级数展开式的一阶和二阶项的系数。 泰勒级数有更多项，因此也有更多系数（C、D、...），但很少使用。 下表显示了生物介质中非线性参数的典型值。

在液体中，通常使用修改后的系数，称为 β = 1 + B 2 A

如果去掉压力泰勒展开式中的第二项，就可以推导出粘性波动方程。 如果保留它，压力中的非线性项将出现在 Westervelt 方程中。

其中 p是声压，c 0 是小信号声速，δ 是声音扩散率，β 是非线性系数， ρ 0 是环境密度。