弛豫时间
编辑在物理科学中,松弛通常意味着扰动系统恢复到平衡状态。每个松弛过程都可以按松弛时间 τ 进行分类。 松弛作为时间 t 函数的最简单的理论描述是指数定律 exp(−t/τ)(指数衰减)。
在简单的线性系统中
编辑力学:阻尼非受迫振荡器
编辑设齐次微分方程:
m d 2 y d t 2 + γ d y d t + k y = 0 {dISPlaystyle m{frac {d{2}y}{dt{2}}}+gamma {frac {dy}{dt}}+ ky=0}
模型阻尼弹簧上重物的非受迫振荡。
位移的形式为 y ( t ) = A e − t / T cos ( μ t − δ ) {diSPlaystyle y(t)=Ae{-t/T}cos(mu t-delta )} 。 常数 T ( = 2 m / γ {displaystyle =2m/gamma } ) 称为系统的弛豫时间,常数 μ 是准频率。
电子:RC电路
编辑V ( t ) = V 0 e − t R C , {displaystyle V(t)=V_{0}e{-{frac {t}{RC}}} ,}
常数 τ = R C {displaystyle tau =RC } 称为电路的弛豫时间或 RC 时间常数。 由电容器通过电阻重复放电产生重复波形的非线性振荡器电路称为张弛振荡器。
凝聚态物理
编辑在凝聚态物理学中,弛豫通常被研究为对小的外部扰动的线性响应。 由于潜在的微观过程即使在没有外部扰动的情况下也是活跃的,因此还可以研究平衡状态下的弛豫,而不是通常进入平衡状态的弛豫(参见波动耗散定理)。
压力放松
编辑介电弛豫时间
编辑在介电材料中,介电极化 P 取决于电场 E。如果 E 发生变化,P(t) 会做出反应:极化会松弛到新的平衡状态。 它在介电光谱学中很重要。 非常长的弛豫时间是介电吸收的原因。
介电弛豫时间与电导率密切相关。 在半导体中,它衡量通过传导过程被中和所需的时间。 这种弛豫时间在金属中很小,在半导体和绝缘体中可能很大。
液体和无定形固体
编辑无定形固体如无定形吲哚美辛表现出分子运动的温度依赖性,这可以量化为固体在亚稳态过冷液体或玻璃中接近晶体分子运动特征的平均弛豫时间。 差示扫描量热法可用于量化由于分子结构松弛引起的焓变。
结构弛豫一词于 1947/48 年在科学文献中引入,没有任何解释,适用于 NMR,与热弛豫的含义相同。
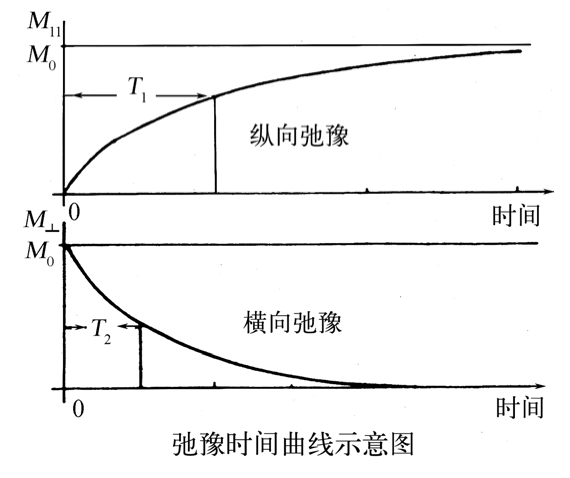
核磁共振中的自旋弛豫
编辑在核磁共振 (NMR) 中,各种弛豫是它测量的特性。
化学松弛法
编辑在化学动力学中,弛豫方法用于测量非常快的反应速率。 最初处于平衡状态的系统会因参数的快速变化而受到干扰,例如温度(最常见)、压力、电场或溶剂的 pH 值。 然后通常通过光谱手段观察恢复平衡,并测量弛豫时间。 结合系统的化学平衡常数,这可以确定正向和反向反应的速率常数。
单分子一级可逆反应
编辑接近平衡的单分子一级可逆反应可以通过以下符号结构可视化:A → k B → k ′ A {displaystyle {ce {A}}~{overset {k}{ rightarrow }}~{ce {B}}~{overset {k’}{rightarrow }}~{ce {A}}} A ↽ − − ⇀ B {displaystyle {ce {A <=>; B}}}
换句话说,反应物 A 和产物 B 根据反应速率常数 k 和 k’ 相互形成。
为了求解 A 的浓度,认识到正向反应 ( A → k B {displaystyle {ce {A ->[{k}] B}}} ) 导致 A 的浓度随时间降低 ,而逆反应 ( B → k ′ A {displaystyle {ce {B ->[{k’}] A}}} ) 导致 A 的浓度随时间增加。
因此,d [ A ] d t = − k [ A ] + k ′ [ B ] {displaystyle {d{ce {[A]}} over dt}=-k{ce {[A ]}}+k'{ce {[B]}}} ,其中 A 和 B 周围的括号表示浓度。
如果我们说在 t = 0 , [ A ] ( t ) = [ A ] 0 {displaystyle t=0,{ce {[A]}}(t)={ce {[A] }}_{0}} ,并应用质量守恒定律。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/216778/
