哈密顿-雅可比方程

积分级数矢量多变量高级

专门

• 小数
• 马利亚文
• 随机
• 变化

各种各样的

• 初等数学
• 历史
• 词汇表
• 主题列表
• 整合蜜蜂
• 数学分析

• v
• t
• e

在物理学中，以威廉·罗文·汉密尔顿和卡尔·古斯塔夫·雅各布·雅可比命名的哈密顿-雅可比方法是经典力学的替代公式，等同于牛顿运动定律、拉格朗日力学和哈密顿力学等其他公式。 哈密顿-雅可比方程序在确定机械系统的守恒量方面特别有用，即使机械问题本身无法完全解决，这也是可能的。

哈密顿-雅可比方也是xxx一个可以将粒子的运动表示为波的力学公式。 从这个意义上说，它实现了理论物理学的一个长期目标（至少可以追溯到 18 世纪的约翰·伯努利），即找到光的传播与粒子运动之间的类比。 机械系统遵循的波动方程与薛定谔方程相似，但不完全相同，如下所述； 出于这个原因，哈密顿-雅可比方程序被认为是经典力学最接近量子力学的方法。

在数学中，哈密顿-雅可比方是变分法问题推广中描述极值几何的必要条件。 可以理解为动态规划中Hamilton-Jacobi-Bellman方程的特例。

粗体字变量，例如 q {\displaystyle \mathbf {q} } 表示 N {\displaystyle N} 广义坐标的列表，

q = ( q 1 , q 2 , … , q N − 1 , q N ) {\displaystyle \mathbf {q} =(q_{1},q_{2},\ldots ,q_{N-1 },q_{N})}

变量或列表上的点表示时间导数（参见牛顿符号）。 例如，

q ˙ = d q d t 。 {\displaystyle {\dot {\mathbf {q} }}={\frac {d\mathbf {q} }{dt}}。}

坐标数相同的两个列表之间的点积表示法是对应分量乘积之和的简写，如

p ⋅ q = ∑ k = 1 N p k q k 。 {\displaystyle \mathbf {p} \cdot \mathbf {q} =\sum _{k=1}{N}p_{k}q_{k}。}

让 Hessian 矩阵 H L ( q , q ˙ , t ) = { ∂ 2 L / ∂ q ˙ i ∂ q ˙ j } i j {\textstyle H_{\cal {L}}(\mathbf {q} , \mathbf {\dot {q}} ,t)=\left\{\partial {2}{\cal {L}}/\partial {\dot {q}}{i} \partial {\dot {q}}{j}\right\}_{ij}} 是可逆的。 关系

d d t ∂ L ∂ q ˙ i = ∑ j = 1 n ( ∂ 2 L ∂ q ˙ i ∂ q ˙ j q ¨ j + ∂ 2 L ∂ q ˙ i ∂ q j q ˙ j ) + ∂ 2 L ∂ q ˙ i ∂ t , i = 1 , … , n , {\displaystyle {\frac {d}{dt}}{\frac {\partial {\cal {L}}}{\partial {\dot { q}}{i}}}=\sum _{j=1}{n}\left({\frac {\partial {2}{\cal {L}}}{\partial { \dot {q}}{i}\partial {\dot {q}}{j}}}{\ddot {q}}{j}+{\frac {\partial {2}{ \cal {L}}}{\partial {\dot {q}}{i}\partial {q}{j}}}{\dot {q}}{j}\right)+ {\frac {\partial {2}{\cal {L}}}{\partial {\dot {q}}{i}\partial t}},\qquad i=1, ldots ,n,}

表明欧拉-拉格朗日方程构成了一个 n × n {\displaystyle n\times n} 二阶常微分方程组。 反转矩阵 H L {\displaystyle H_{\cal {L}}} 将这个系统转换为

q ¨ i = F i ( q , q ˙ , t ) , i = 1 , … , n 。 {\displaystyle {\ddot {q}}{i}=F_{i}(\mathbf {q} ,\mathbf {\dot {q}} ,t),\ i=1, ldots,n.}

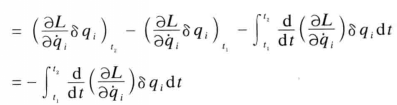
令配置空间中的时刻 t 0 {\displaystyle t_{0}} 和点 q 0 ∈ M {\displaystyle \mathbf {q} _{0}\in M} 固定。 存在xxx性定理保证，对于每个 v 0 ， {\displaystyle \mathbf {v} _{0},} 条件为 γ | 的初始值问题 τ = t 0 = q 0 {\displaystyle \gamma |_{\tau =t_{0}}=\mathbf {q} _{0}} 和 γ ˙ | τ = t 0 = v 0 {\displaystyle {\dot {\gamma }}|_{\tau =t_{0}}=\mathbf {v} _{0}} 有局部xxx解 γ = γ ( τ ; t 0 , q 0 , v 0 ) 。 {\displaystyle \gamma =\gamma (\tau ;t_{0},\mathbf {q} _{0},\mathbf {v} _{0}).} 另外，让有 足够小的时间间隔 ( t 0 , t 1 ) {\displaystyle (t_{0},t_{1})} 使得具有不同初始速度 v 0 {\displaystyle \mathbf {v} _{0 }} 不会在 M × ( t 0 , t 1 ) 中相交。 {\displaystyle M\times (t_{0},t_{1}).} 后者意味着，对于任何 q ∈ M {\displaystyle \mathbf {q} \in M} 和任何 t ∈ ( t 0 , t 1 ) , {\displaystyle t\in (t_{0},t_{1}),} 至多有一个极值 γ = γ ( τ ; t , t 0 , q , q 0 ) {\displaystyle \gamma =\gamma (\tau ;t,t_{0},\mathbf {q} ,\mathbf {q} _{0})} 其中 γ | τ = t 0 = q 0 {\displaystyle \gamma |_{\tau =t_{0}}=\mathbf {q} _{0}} 和 γ | τ = t = q 。