广义坐标

在分析力学中，广义坐标是一组参数，用于表示系统在配置空间中的状态。 这些参数必须xxx地定义系统相对于参考状态的配置。 广义速度是系统广义坐标的时间导数。 形容词 generalized 将这些参数与术语坐标的传统用法区分开来，以指代笛卡尔坐标

广义坐标的一个例子是使用摆相对于垂直方向的角度来描述摆的位置，而不是通过摆的 x 和 y 位置。

尽管物理系统的广义坐标可能有很多可能的选择，但通常选择它们是为了简化计算，例如系统运动方程的求解。 如果坐标相互独立，则独立广义坐标的个数由系统的自由度数定义。

广义坐标与广义动量配对以提供相空间上的规范坐标。

通常选择广义坐标来提供定义系统配置的最少数量的独立坐标，这简化了拉格朗日运动方程的公式。 然而，也可能发生一组有用的广义坐标可能是相关的，这意味着它们由一个或多个约束方程相关。

对于 3D 实坐标空间中的 N 个粒子系统，每个粒子的位置向量可以写成笛卡尔坐标中的三元组：

r 1 = ( x 1 , y 1 , z 1 ) , r 2 = ( x 2 , y 2 , z 2 ) , ⋮ r N = ( x N , y N , z N ) {displaystyle {begin {对齐}&mathbf {r} _{1}=(x_{1},y_{1},z_{1}),&mathbf {r} _{2}= (x_{2},y_{2},z_{2}),&qquad qquad vdots &mathbf {r} _{N}=( x_{N},y_{N},z_{N})end{对齐}}}

任何位置向量都可以表示为 rk，其中 k = 1, 2, …, N 标记粒子。 完整约束是粒子 k 形式的约束方程

f ( r k , t ) = 0 {displaystyle f(mathbf {r} _{k},t)=0}

它将该粒子的所有 3 个空间坐标连接在一起，因此它们不是独立的。 约束可能随时间变化，因此时间 t 将明确出现在约束方程中。 在任何时刻，任何一个坐标都将根据其他坐标确定，例如 如果给定 xk 和 zk，那么 yk 也给定。 一个约束方程算作一个约束。 如果有C个约束，每个都有一个方程，那么就会有C个约束方程。 不一定每个粒子都有一个约束方程，如果系统没有约束，那么也就没有约束方程。

到目前为止，系统的配置由 3N 个数量定义，但可以删除 C 坐标，每个约束方程中的一个坐标。 独立坐标的个数为n = 3N − C。（在D维中，原始配置需要ND个坐标，通过约束减少意味着n = ND − C）。 理想的做法是使用定义整个系统配置所需的最少坐标，同时利用对系统的约束。 这些量在本文中称为广义坐标，表示为 qj(t)。 将它们收集成一个n元组很方便

q ( t ) = ( q 1 ( t ) , q 2 ( t ) , … , q n ( t ) ) {displaystyle mathbf {q} (t)=(q_{1}(t), q_{2}(t), ldots , q_{n}(t))}

这是系统配置空间中的一个点。 它们都是相互独立的，每一个都是时间的函数。 在几何上，它们可以是沿直线的长度，或沿曲线的弧长，或角； 不一定是笛卡尔坐标或其他标准正交坐标。 每个自由度都有一个，因此广义坐标的数量等于自由度的数量 n。 自由度对应于改变系统配置的一个量，例如钟摆的角度，或珠子沿导线穿过的弧长。

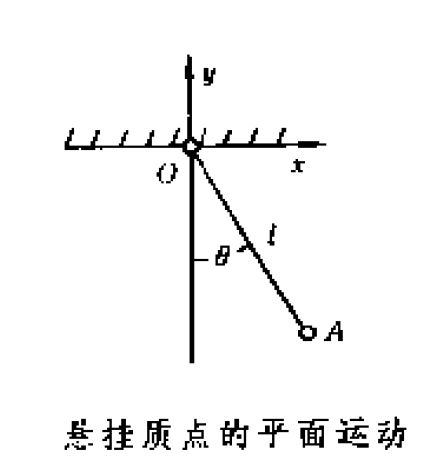
如果可以从约束中找到与自由度一样多的独立变量，则可以将它们用作广义坐标。 粒子 k 的位置向量 rk 是所有 n 个广义坐标（以及通过它们的时间）的函数，

r k = r k ( q ( t ) ) , {displaystyle mathbf {r} _{k}=mathbf {r} _{k}(mathbf {q} (t)),, }

并且广义坐标可以被认为是与约束相关联的参数。

q 的相应时间导数是广义速度，

q ˙ = d q d t = ( q ˙ 1 ( t ) , q ˙ 2 ( t ) , … , q ˙ n ( t ) ) {displaystyle {dot {mathbf {q} }}={ frac {dmathbf {q} }{dt}}=({dot {q}}_{1}(t), {dot {q}。