薛定谔方程

薛定谔方程是控制量子力学系统波函数的线性偏微分方程。 它是量子力学的一个关键成果，它的发现是该学科发展的一个重要里程碑。

从概念上讲，薛定谔方程是经典力学中牛顿第二定律的量子对应物。 给定一组已知的初始条件，牛顿第二定律可以对给定物理系统随时间采取的路径进行数学预测。 薛定谔方程给出了波函数随时间的演变，即孤立物理系统的量子力学表征。 该方程式可以从时间演化算子必须是幺正这一事实得出，因此必须由自伴随算子的指数生成，即量子哈密顿量。

薛定谔方程并不是研究量子力学系统和做出预测的xxx途径。 量子力学的其他公式包括由维尔纳海森堡引入的矩阵力学和主要由理查德费曼开发的路径积分公式。 保罗·狄拉克 (Paul Dirac) 将矩阵力学和薛定谔方程合并到一个公式中。 当比较这些方法时，薛定谔方法的使用有时被称为波浪力学。

物理或化学入门课程通常以一种仅了解基本微积分的概念和符号，特别是空间和时间的导数就可以理解的方式介绍薛定谔方法。

这个向量被假设为在希尔伯特空间的内积下被归一化，也就是说，在狄拉克符号中它服从 ⟨ ψ | ψ ⟩ = 1 。 这个希尔伯特空间的确切性质取决于系统——例如，为了描述位置和动量，希尔伯特空间是复杂平方可积函数的空间 L 2 ( C ) ，而单个质子自旋的希尔伯特空间只是二维复数向量空间 C 2 与通常的内积。

感兴趣的物理量——位置、动量、能量、自旋——由可观察量表示，这些可观察量是作用于希尔伯特空间的厄米特线性算子。 一个波函数可以是一个可观测值的特征向量，在这种情况下它被称为一个特征态，相关的特征值对应于该特征态下可观测值的值。 更一般地，量子态将是本征态的线性组合，称为量子叠加。

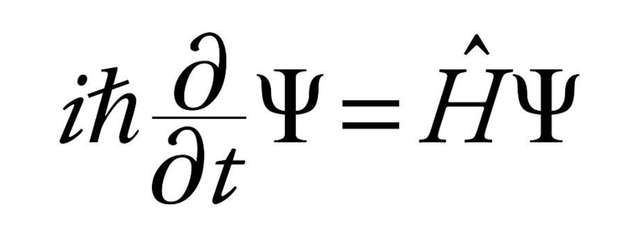
当一个可观察量被测量时，结果将是其特征值之一，其概率由 Born 规则给出：在最简单的情况下，特征值 λ 是非退化的，概率由 | 给出 ⟨ λ | ⟩ | 2 ，其中 | λ ⟩ 是其关联的特征向量。 更一般地，特征值是退化的，概率由 ⟨ ψ | 给出 λ | ψ ⟩ ，其中 P λ 是投影到其关联的特征空间上。

动量本征态是无限范围的完美单色波，它不是平方可积的。