瑞利数

在流体力学中，流体的瑞利数（Ra，以瑞利勋爵命名）是与浮力驱动流相关的无量纲数，也称为自由（或自然）对流。 它表征流体的流态：在一定的较低范围内的值表示层流； 在较高范围内的值，湍流。 在某个临界值以下，没有流体运动，传热是通过传导而不是对流进行的。 对于大多数工程目的，瑞利数很大，大约在 106 到 108 之间。

瑞利数定义为描述流体内浮力和粘度之间关系的格拉斯霍夫数 (Gr) 与描述动量扩散率和热扩散率之间关系的普朗特数 (Pr) 的乘积：Ra = Gr×Pr。 因此，它也可以被视为浮力与粘性力之比乘以动量与热扩散率之比：Ra = B/μ × ν/α。 它与努塞尔数（Nu）密切相关。

瑞利数描述了当流体的质量密度不均匀时流体（例如水或空气）的行为。 质量密度差异通常是由温度差异引起的。 通常，流体在受热时会膨胀并变得不那么稠密。 重力导致流体中密度较大的部分下沉，这称为对流。 Rayleigh 勋爵研究了 Rayleigh-Bénard 对流的情况。 当瑞利数 Ra 低于流体的临界值时，没有流动，传热完全通过传导进行； 当它超过该值时，热量通过自然对流传递。

当质量密度差异由温差引起时，根据定义，Ra 是速度为 u {dISPlaystyle u} 的扩散热传输的时间尺度与对流热传输的时间尺度之比：

R a = 通过扩散进行热传输的时间尺度 通过对流以速度 u 进行热传输的时间尺度。 {diSPlaystyle mathrm {Ra} ={frac {mbox{通过扩散进行热传输的时间尺度}}{{mbox{通过对流进行热传输的时间尺度}}~u}} .}

这意味着瑞利数是佩克莱数的一种。 对于在所有三个维度上大小为 l {displaystyle l} 且质量密度差为 Δ ρ {displaystyle Delta rho } 的流体，重力的量级为 Δ ρ l 3 g {displaystyle Delta rho l{3}g} ，其中 g {displaystyle g} 是重力加速度。 根据 Stokes 方程，当流体体积下沉时，粘性阻力的阶数为 η l u {displaystyle eta lu} ，其中 η {displaystyle eta } 是流体的动态粘度。 当这两个力相等时，速度 u ∼ Δ ρ l 2 g / η {displaystyle usim Delta rho l{2}g/eta } 。 因此，通过流动传输的时间尺度是 l / u ∼ η / Δ ρ l g {displaystyle l/usim eta /Delta rho lg} 。 跨越距离 l {displaystyle l} 的热扩散的时间尺度是 l 2 / α {displaystyle l{2}/alpha } ，其中 α {displaystyle alpha } 是热扩散率。 因此瑞利数 Ra 是

R a = l 2 / α η / Δ ρ l g = Δ ρ l 3 g η α = ρ β Δ T l 3 g η α {displaystyle mathrm {Ra} ={frac {l{2} /alpha }{eta /Delta rho lg}}={frac {Delta rho l{3}g}{eta alpha }}={ frac {rho beta Delta Tl{3}g}{eta alpha }}}

其中我们对平均质量密度为 ρ {displaystyle rho 的流体近似密度差 } ，热膨胀系数 β {displaystyle beta } 和跨越距离 l {displaystyle l} 的温差 Δ T {displaystyle Delta T} 。

瑞利数可以写成 Grashof 数和 Prandtl 数的乘积：

R a = G r P r 。 {displaystyle mathrm {Ra} =mathrm {Gr} mathrm {Pr} .}

对于垂直壁附近的自由对流，瑞利数定义为：

R a x = g β ν α ( T s − T ∞ ) x 3 = G r x P r {displaystyle mathrm {Ra} _{x}={frac {gbeta }{nu alpha }}(T_{s}-T_{infty })x{3}=mathrm {Gr} _{x}mathrm {Pr} }

在哪里：

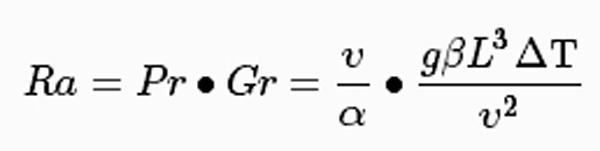
x 是特征长度Rax 是特征长度的瑞利数 xg 是重力加速度β 是热膨胀系数（等于 1/T，对于理想气体，其中 T 是绝对温度）。ν {displaystyle nu }是运动粘度α是热扩散系数Ts是表面温度T∞是静止温度（远离物体表面的流体温度）Grx是特征长度的格拉斯霍夫数xPr是普朗特数

在上文中，流体特性 Pr、ν、α 和 β 在薄膜温度下进行评估，其定义为：

T f = T s + T ∞ 2 。 {displaystyle T_{f}={frac {T_{s}+T_{infty }}{2}}。}

对于均匀的壁热通量，修改后的瑞利数定义为：

R a x ∗ = g β q o ″ ν α k x 4 {displaystyle mathrm {Ra} _{x}{*}={frac {gbeta q''_{o}}{ nu alpha k}}x{4}}。