胡克定律

在物理学中，胡克定律是一个经验法则，它指出将弹簧拉伸或压缩一定距离 (x) 所需的力 (F) 与该距离成线性比例关系，即 Fs = kx，其中 k 是 a 弹簧的常数因子特性（即其刚度），并且 x 与弹簧的总可能变形相比较小。

胡克方程在弹性体变形的许多其他情况下（在某种程度上）成立，例如风吹过高楼，音乐家拨动吉他弦。 可以假设该方程的弹性体或材料被称为线性弹性或胡克。

胡克定律只是弹簧和其他弹性体对所施加力的真实响应的一阶线性近似。 一旦力超过某个极限，它最终肯定会失效，因为没有任何材料可以被压缩超过某个最小尺寸，或被拉伸超过xxx尺寸，而不会发生一些xxx变形或状态变化。 在达到这些弹性极限之前，许多材料会明显偏离胡克定律。

另一方面，只要力和变形足够小，胡克定律是大多数固体的精确近似。 正因如此，胡克定律被广泛应用于科学和工程的各个分支，是地震学、分子力学和声学等许多学科的基础。 它也是弹簧秤、压力计、检流计和机械钟摆轮背后的基本原理。

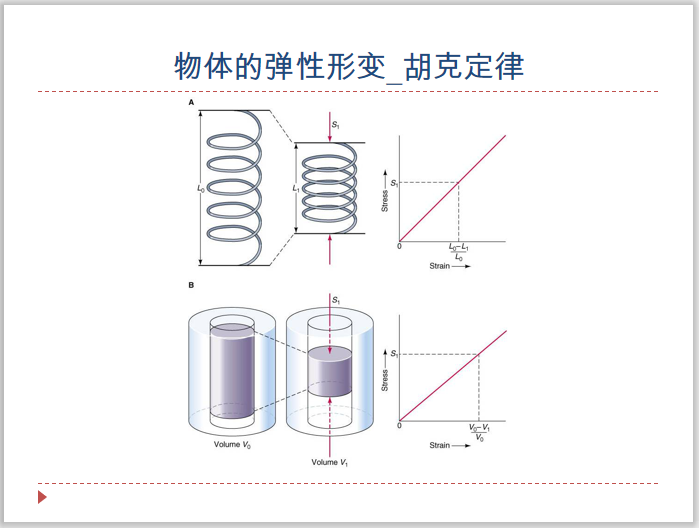
现代弹性理论将胡克定律概括为：弹性物体或材料的应变（变形）与施加在其上的应力成正比。 然而，由于一般的应力和应变可能有多个独立的分量，比例因子可能不再只是一个单一的实数，而是一个可以用实数矩阵表示的线性映射（张量）。

在这种一般形式下，胡克定律可以根据构成复杂物体的材料的内在特性来推断其应变和应力之间的关系。 例如，可以推断出具有均匀横截面的均质杆在拉伸时将表现得像一个简单的弹簧，其刚度 k 与其横截面积成正比，与其长度成反比。

考虑一个简单的螺旋弹簧，它的一端连接到某个固定物体，而自由端被一个大小为 Fs 的力拉动。 假设弹簧已达到平衡状态，其长度不再变化。 令 x 为弹簧自由端从其松弛位置（未拉伸时）的位移量。 此外，当弹簧被压缩时，同样的公式成立，此时 Fs 和 x 均为负值。 根据这个公式，施加的力 Fs 作为位移 x 的函数的图形将是一条通过原点的直线，其斜率为 k。

弹簧的胡克定律有时（但很少）根据约定说明 Fs 是弹簧施加在拉动其自由端的任何物体上的恢复力。

胡克弹簧定律通常适用于任何具有任意复杂性的弹性物体，只要变形和应力都可以用一个既可以是正数也可以是负数的数字来表示。