混沌理论

混合理论是一个跨学科的科学研究领域和数学分支，专注于动力系统的基本模式和确定性定律，这些动力系统对初始条件高度敏感，曾被认为具有完全随机的无序和不规则状态。 混合理论指出，在混沌复杂系统的明显随机性中，存在潜在的模式、相互联系、不断的反馈循环、重复、自相似性、分形和自组织。 蝴蝶效应是混沌的一个基本原理，它描述了确定性非线性系统的一个状态的微小变化如何导致后来状态的巨大差异（意味着对初始条件的敏感依赖性）。 这种行为的一个比喻是，一只蝴蝶在巴西扇动翅膀可能会在德克萨斯州引发龙卷风。

初始条件的微小差异，例如由于测量误差或数值计算中的舍入误差引起的差异，可能会为此类动力系统产生大相径庭的结果，从而导致对其行为的长期预测通常是不可能的。 即使这些系统是确定性的，这也可能发生，这意味着它们未来的行为遵循独特的演化，完全由它们的初始条件决定，不涉及随机因素。 换句话说，这些系统的确定性并不能使它们变得可预测。 这种行为被称为确定性混沌，或简称为混沌。 Edward Lorenz 将该理论总结为：

混沌：现在决定未来，但近似的现在不近似决定未来。

混沌行为存在于许多自然系统中，包括流体流动、心跳不规则、天气和气候。 它也会在一些具有人工成分的系统中自发发生，例如道路交通。 可以通过混沌数学模型的分析，或通过递归图和庞加莱图等分析技术来研究这种行为。 混合理论在多种学科中都有应用，包括气象学、人类学、社会学、环境科学、计算机科学、工程学、经济学、生态学和大流行危机管理。 该理论为复杂动力系统、混沌边缘理论和自组装过程等研究领域奠定了基础。

混合理论涉及确定性系统，其行为在原则上是可以预测的。 混沌系统在一段时间内是可预测的，然后“看起来”变得随机了。 可以有效预测混沌系统行为的时间长短取决于三件事：预测中可以容忍多少不确定性，可以多准确地测量其当前状态，以及取决于系统动态的时间尺度 系统，称为李亚普诺夫时间。 Lyapunov 时间的一些例子是：混沌电路，大约 1 毫秒； 天气系统，几天（未经证实）； 太阳系内部，四五百万年。 在混沌系统中，预测的不确定性随着时间的推移呈指数增长。 因此，从数学上讲，将预测时间加倍大于预测中比例不确定性的平方。 这意味着，在实践中，无法在超过李雅普诺夫时间的两倍或三倍的时间间隔内做出有意义的预测。 当无法做出有意义的预测时，系统就会显得随机。

混合理论是一种定性和定量分析方法，用于研究动态系统的行为，这些行为不能由单一的数据关系来解释和预测，而必须由整体的、连续的数据关系来解释和预测。

在通常的用法中，混沌意味着一种混乱的状态。 然而，在混沌理论中，该术语的定义更为精确。 尽管不存在普遍接受的混沌数学定义，但最初由 Robert L. Devaney 制定的常用定义表示，要将动力系统归类为混沌，它必须具有以下属性：

• 它必须对初始条件敏感，
• 它必须是拓扑传递的，
• 它必须有密集的周期轨道。

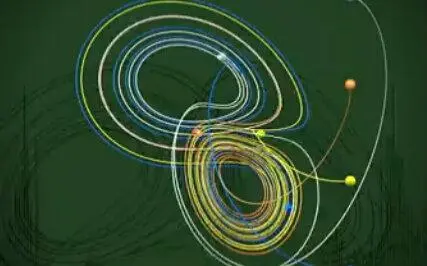
在某些情况下，上面的最后两个属性实际上暗示了对初始条件的敏感性。 在离散时间的情况下，这适用于度量空间上的所有连续映射。 在这些情况下，虽然它通常是最实际重要的属性，但无需在定义中说明对初始条件的敏感性。

如果注意力仅限于间隔，则第二个属性意味着其他两个。 混沌的另一种通常较弱的定义仅使用上面列表中的前两个属性。

对初始条件的敏感性意味着混沌系统中的每个点都被其他具有显着差异的点任意逼近。