相对论角动量

在物理学中，相对论角动量是指狭义相对论 (SR) 和广义相对论 (GR) 中定义角动量的数学形式和物理概念。 相对论量与经典力学中的三维量略有不同。

角动量是从位置和动量导出的重要动力学量。 它是衡量物体的旋转运动和对其旋转变化的抵抗力的量度。 同样，动量守恒对应于平移对称，角动量守恒对应于旋转对称——对称性和守恒定律之间的联系是由诺特定理建立的。 虽然这些概念最初是在经典力学中发现的，但它们在狭义相对论和广义相对论中也是真实且重要的。 在抽象代数方面，角动量、四动量和其他时空对称性的不变性由洛伦兹群或更一般的庞加莱群描述。

通过实施相对论假设，在经典物理学中保持独立的物理量在 SR 和 GR 中自然地结合在一起。 最值得注意的是，空间和时间坐标组合成四位，能量和动量组合成四动量。这四个向量的分量取决于所使用的参考系，并在洛伦兹变换下改变为其他惯性系或加速系。

相对论角动量不太明显。 角动量的经典定义是位置 x 与动量 p 的叉积得到伪向量 x × p，或者作为外积得到二阶反对称张量 x ∧ p。 如果有的话，这与什么结合？ 还有一个不常被讨论的向量——它是与系统质心提升相关的质量极向量的时变矩（不是惯性矩），它结合了经典的角动量伪向量形成二阶反对称张量，与电场极矢量与磁场伪矢量结合形成电磁场反对称张量的方式完全相同。对于旋转的质能分布（如陀螺仪、行星、恒星和黑洞）而不是点状粒子，角动量张量用旋转物体的应力能量张量表示。

仅在狭义相对论中，在旋转物体的静止系中，存在类似于量子力学和相对论量子力学中的自旋的固有角动量，尽管是针对扩展体而不是点粒子。

在相对论量子力学中，基本粒子具有自旋，这是对轨道角动量算子的额外贡献，产生总角动量张量算子。在任何情况下，物体轨道角动量的固有自旋加法都可以用 Pauli-Lubanski 伪向量表示。

作为参考和背景，给出了两种密切相关的角动量形式。

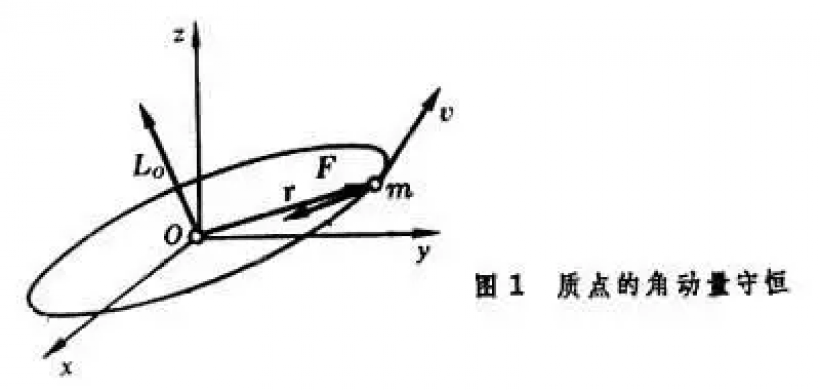
在经典力学中，瞬时三维位置向量x=(x,y,z)和动量向量p=(px,py,pz)的粒子的轨道角动量定义为轴向向量L=x× p {displaystyle mathbf {L} =mathbf {x} times mathbf {p} } 它具有三个分量，由笛卡尔方向的循环排列系统地给出（例如，将 x 更改为 y， y 到 z，z 到 x，重复）L x = y p z − z p y ，L y = z p x − x p z ，L z = x p y − y p x 。

一个相关的定义是将轨道角动量视为一个平面元素。 这可以通过用外代数语言中的外积代替叉积来实现，角动量变成逆变二阶反对称张量 L = x ∧ p {displaystyle mathbf {L} =mathbf { x} 楔形 mathbf {p} }

或者写成 x = (x1, x2, x3) = (x, y, z) 和动量向量 p = (p1, p2, p3) = (px, py, pz)，这些分量可以用张量索引符号紧凑地缩写 L i j = x i p j − x j p i {displaystyle L{ij}=x{i}p{j}-x{j}p{i}} 其中索引 i 和 j 取值 1、2、3。