物种面积曲线

物种-面积关系或物种-面积曲线描述了栖息地或部分栖息地的面积与该区域内发现的物种数量之间的关系。 更大的区域往往包含更多的物种，根据经验，相对数量似乎遵循系统的数学关系。 物种-面积关系通常是针对单一类型的生物构建的，例如特定地点内的所有维管植物或特定营养级的所有物种。 如果仅仅因为庞大的数据要求，它很少（如果有的话）为所有类型的生物构建。 它与物种发现曲线相关但不完全相同。

生态学家提出了一系列决定物种-面积关系的斜率和高度的因素。 这些因素包括移民和灭绝之间的相对平衡、小区域与大区域干扰的速度和幅度、捕食者-猎物动态，以及由于扩散限制或栖息地异质性导致的同一物种个体的聚集。 物种-面积关系被认为遵循热力学第二定律。 与这些机械解释相反，其他人断言需要测试模式是否只是随机抽样过程的结果。 物种-区域关系通常在保护科学中进行评估，以预测栖息地丧失和栖息地破碎化情况下的灭绝率。

作者根据采样的栖息地类型和使用的普查设计对物种-面积关系进行了分类。 物种-区域关系理论的早期研究者 Frank W. Preston 将其分为两种类型：样本（对生长在普查区的连续栖息地的普查，也称为大陆物种-区域关系）和隔离物 （不连续栖息地的普查，例如岛屿，也称为岛屿物种-区域关系）。 Michael Rosenzweig 还指出，非常大的区域（包括不同的生物地理省份或大陆）的物种-区域关系与岛屿或较小的毗连区域的物种-区域关系表现不同。 据推测，岛屿类物种-区域关系的斜率（在对数-对数空间中）比大陆关系更陡，但 2006 年对近 700 个物种-区域关系的荟萃分析发现前者的斜率低于后者。

无论普查设计和栖息地类型如何，物种-面积关系通常都配备一个简单的函数。 弗兰克·普雷斯顿 (Frank Preston) 提倡幂函数是基于他对对数正态物种丰度分布的研究。 若S {displaystyle S}为物种数，A {displaystyle A}为栖息地面积，z {displaystyle z}为对数-对数空间中物种面积关系的斜率，则 幂函数物种面积关系如下：

S = c A z {displaystyle S=cA{z}}

这里的 c {displaystyle c} 是一个常数，它取决于面积测量所用的单位，并且等于如果栖息地面积被限制在一个平方单位内将会存在的物种数量。

它看起来像半对数轴上的一条直线，其中记录了面积并且物种数量是算术数。 在任何一种情况下，当用算术图绘制时，物种-面积关系几乎总是在减速（具有负二阶导数）。

物种-面积关系通常针对不同大小的岛屿（或彼此隔离的栖息地，例如农业景观中的林地）绘制。 虽然较大的岛屿往往拥有更多的物种，但较小的岛屿可能比较大的岛屿拥有更多的物种。 相比之下，相邻栖息地的物种-面积关系将始终随着面积的增加而上升，前提是样本地块相互嵌套。

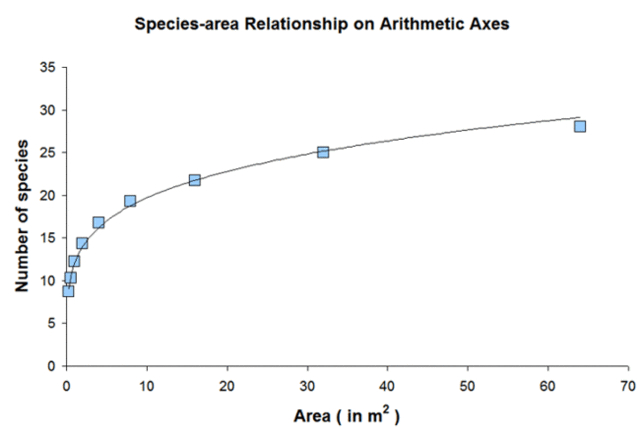
大陆地区（相邻栖息地）的物种-面积关系将根据用于构建它的普查设计而有所不同。 一种常用的方法是使用大小依次变大的样方，这样每个样方所包围的面积就包括较小样方所包围的面积（即嵌套区域）。

在 20 世纪上半叶，植物生态学家经常使用物种面积曲线来估计充分描述群落所需的样方的最小大小。 这是通过绘制曲线（通常在算术轴上，而不是对数-对数或半对数轴）并估计使用更大的样方后仅增加几个物种的面积来完成的。 这称为最小面积。