单向函数

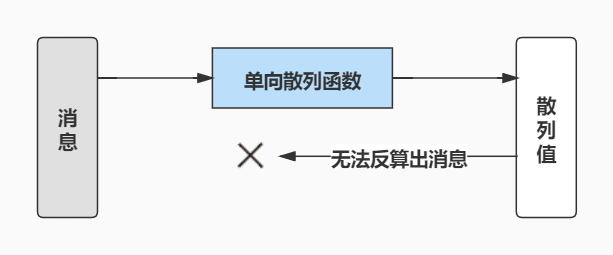
在计算机科学中，单向函数是一种数学函数，根据复杂性理论“容易”计算，但“难以”逆转。 在广义上，函数也以这种方式指定，其中已知无法在合理的时间内执行反演。

一个很好的例子是大城市的经典纸质电话簿：如果您知道名字，您可以快速找到相应的电话号码。 但是，如果只知道电话号码，要查找关联的姓名是非常耗时的。

单向数构成了非对称密码系统的基础。

数学单向数 f 必须具有以下性质：

• 计算给定 x 的函数值 y = f ( x )是“简单的”，即。 也就是说，有一种算法可以在多项式时间内计算它。
• 函数的反函数i的计算。给定 y 的原像 x 使得 f ( x ) = y  是困难的，也就是说，没有概率算法 F在多项式时间内运行并以不可忽略的概率输出输入图像的原像。更准确地说，以下适用于每个概率算法 F具有合适的输入和输出格式：对于每个 c ∈ N

不知道是否有满足单向条件的函数。 事实上，证明它们的存在意味着同时证明P≠NP。 反之，单向函数的存在不符合P≠NP：概率算法也可以用来反转函数。 为了使逆过程足够低效，NP 不能是复杂类 BPP 的子集。

单向数对密码学中的应用程序特别感兴趣。 然而，对于这样的用途，就复杂性理论而言，另一个要求是必要的：所提到的复杂性类别考虑了最坏情况（worst case），即算法的最长运行时间。 对于密码应用程序，算法在一般情况下也必须是低效的。

密码中有一个单向函数的直接应用。 这些通常不会直接保存，而是作为密码哈希函数的输出，在其中输入密码（通常用盐作为补充）。 登录时的检查不是通过比较明文密码而是哈希值来执行的。 因此，管理员或具有系统访问权限的未授权人员永远无法读取用户的密码。 充其量，他可以使用 crack 之类的程序尝试可能的密码。 加密哈希函数的行为类似于单向函数，更准确地说：没有已知的方法可以有效地计算给定输出的输入（原像攻击）。

在实践中，已知的函数到目前为止已经充分满足了单向函数的要求。 不过，要将它们反转是否真的“难”，目前还无法证明。 这种函数的一个例子是两个大质数的乘法，因为质因数分解被认为是一个“困难”的问题。 另一个例子是模幂及其倒数，即离散对数。

单向函数的一个变体是陷门单向函数，也称为陷门函数。 如果您有某些附加信息，这些只能有效地逆转。 Trapdoor 函数用于非对称加密方法，例如 RSA。 活板门功能的类比是金库的功能：任何人都可以锁定金库中的物品。 另一方面，把它拿出来几乎是不可能的——除非你有钥匙/钥匙组合。

以下函数在扩展意义上称为单向函数，目前尚无有效的反演：

• 像 SHA-2 这样的加密散列函数
• 的两个素数或两个整数的乘法很容易，而逆向素因数分解则很困难
• 如果选择适当的群，计算有限群元素的 n 次方很容易，而通过计算离散对数求指数则很复杂