树状自动机
编辑树状自动机是一种类型的状态机。树状自动机处理的是树状结构,而不是更传统的状态机的字符串。下面的文章涉及到分支树自动机,它对应于树的规则语言。与经典自动机一样,有限树自动机(FTA)可以是确定性自动机,也可以不是。根据自动机处理输入树的方式,有限树自动机可以有两种类型:(a)自下而上,(b)自上而下。这是一个重要的问题,因为尽管非确定性(ND)自上而下和ND自下而上的树自动机在表达能力上是相等的,但是确定性自上而下的自动机严格来说比确定性自下而上的自动机要差,因为确定性自上而下的树自动机所指定的树属性只能依赖于路径属性。(确定性的自下而上的树自动机与ND树自动机一样强大)。
树状自动机的定义
编辑F上的自下而上有限树自动机被定义为一个元组(Q,F,Qf,Δ),其中Q是一组状态,F是一个有等级的字母表。
也就是说,Δ的成员是重写规则,从节点的子根是状态,到节点的根是状态。因此,一个节点的状态是由其子节点的状态推导出来的。对于n=0,即对于常量符号f,上述过渡规则的定义为f()→q(f());为了方便,通常省略空括号:f→q(f)。由于这些常量符号(叶子)的过渡规则不需要状态,所以不需要明确定义初始状态。一个自下而上的树状自动机在F上运行一个基础项,同时从其所有叶子开始并向上移动,将Q的一个运行状态与每个子项关联。如果该项根与Qf的一个接受状态关联,则被接受。F上的自上而下的有限树自动机被定义为一个元组(Q,F,Qi,Δ),与自下而上的树自动机有两个区别。
一个自上而下的自动机从根部的一些初始状态开始,沿着树的分支向下移动,沿着运行与每个子项归纳地关联一个状态。如果每个分支都能以这种方式通过,那么一棵树就被接受。
如果没有两个来自Δ的规则具有相同的左手边,则树状自动机被称为确定性的。非确定性自上而下的树状自动机与非确定性自下而上的树状自动机具有相同的表达能力;过渡规则被简单地颠倒,最终状态成为初始状态。相比之下,确定性的自上而下的树形自动机比自下而上的自动机功能要小,因为在确定性的树形自动机中,没有两个过渡规则的左手边是相同的。对于树状自动机,过渡规则是重写规则;而对于自上而下的自动机,左侧将是父节点。因此,确定性的自上而下的树型自动机只能测试在所有分支中都是真的树型属性,因为要写入每个子分支的状态的选择是在父节点决定的,而不知道子分支的内容。
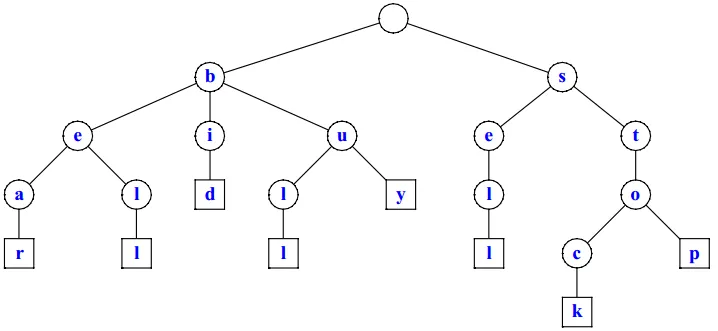
自上而下接受二进制符号中3的倍数的自动机
编辑使用与上面相同的着色,这个例子显示了树形自动机是如何概括普通字符串自动机的。有限确定性字符串自动机接受所有表示3的倍数的二进制数字串。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/163354/
