图形编辑距离

在数学和计算机科学中，图形编辑距离（GED）是衡量两个图形之间的相似性（或不相似性）。图形编辑距离的概念最早是由AlbertoSanfeliu和King-SunFu在1983年以数学形式正式提出的。

图形编辑距离的一个主要应用是在不精确的图形匹配中，如机器学习中的容错模式识别。两个图之间的图编辑距离与字符串之间的编辑距离有关。

由于字符串被解释为最 大度数为1的连接的有向无环图，经典的编辑距离定义如Levenshtein距离、Hamming距离和Jaro-Winkler距离可以被解释为适当约束的图之间的图编辑距离。同样地，图编辑距离也是有根树之间的树编辑距离的泛化。

图编辑距离的数学定义取决于它所定义的图的定义，即图的顶点和边是否被标记以及如何标记，边是否是有方向的。一般来说，给定一组图编辑操作（也被称为基本图操作），两个图之间的图编辑距离基本图编辑操作的集合通常包括。

顶点插入，在图中引入一个新的有标签的顶点。

顶点删除，从图中删除一个单一的（通常是断开的）顶点。

顶点替换，改变给定顶点的标签（或颜色）。

边插入，在一对顶点之间引入一条新的彩色边。

边删除，在一对顶点之间删除一条边。

边替换，改变一个给定边的标签（或颜色）。

其他的，但不太常见的操作，包括诸如边的分割，在一条边上引入一个新的顶点（也创造了一条新的边），以及边的收缩，在边（相同颜色的）之间消除二度的顶点。

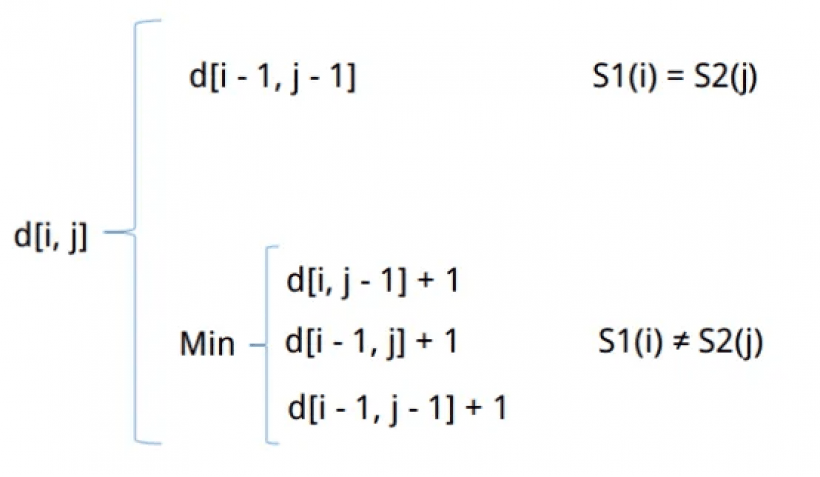
尽管这种复杂的编辑操作可以用更基本的变换来定义，但使用它们可以使成本函数的参数化更加精细c{displaystylec}。当运算符比它的组成成分的总和更便宜时。

对基本的图编辑算子的深入分析见于《图编辑》。并提出了一些方法来自动推导这些基本的图编辑算子。还有一些算法在线学习这些成本。应用图形编辑距离在手写识别、指纹识别和化学信息学中得到了应用。

计算一对图之间的图编辑距离的精确算法通常将问题转化为寻找两个图之间的最小成本编辑路径的问题。最佳编辑路径的计算被视为寻路搜索或最短路径问题，通常以A*搜索算法实现。除了精确的算法外，还有一些有效的近似算法也是已知的。