快速傅里叶变换

快速傅里叶变换（FFT）是一种计算序列的离散傅里叶变换（DFT）或其逆（IDFT）的算法。

傅里叶分析将一个信号从其原始域（通常是时间或空间）转换为频域的表示，反之亦然。DFT是通过将一个数值序列分解为不同频率的成分而得到的。这种操作在许多领域都很有用，但直接从定义中计算它往往太慢而不实用。FFT通过将DFT矩阵分解为稀疏（大部分为零）因子的乘积来快速计算这种转换。因此，它设法将计算DFT的复杂性从是数据大小。

速度上的差异可能是巨大的，特别是对于N可能是数千或数百万的长数据集。在存在舍入误差的情况下，许多FFT算法比直接或间接地评估DFT定义要准确得多。有许多不同的FFT算法，基于广泛的已发表的理论，从简单的复数运算到群论和数论。

快速傅里叶变换被广泛用于工程、音乐、科学和数学领域的应用。其基本思想在1965年得到普及，但一些算法早在1805年就已得出。1994年，吉尔伯特-斯特朗将FFT描述为我们一生中最重要的数字算法，它被IEEE杂志《科学与工程计算》列入20世纪十大算法。

最著名的FFT算法取决于N的因式分解，但是对于所有的N，甚至素数N，都有复杂度为O(NlogN)的FFT。是统一的N次方原始根，因此可以应用于任何有限域的类似变换，如数论变换。由于逆DFT与DFT相同，但指数中的符号相反，且有1/N的因子，任何FFT算法都可以很容易地适用于它。

DFT的快速算法的发展可以追溯到卡尔-弗里德里希-高斯在1805年未发表的工作，当时他需要它来从样本观测中插补小行星帕拉斯和朱诺的轨道。他的方法与JamesCooley和JohnTukey在1965年发表的方法非常相似，他们被认为是现代通用FFT算法的发明者。

虽然高斯的工作甚至早于约瑟夫-傅里叶在1822年的成果，但他没有分析计算时间，最终使用其他方法来实现他的目标。从1805年到1965年，其他作者发表了一些FFT的版本。FrankYates在1932年发表了他的版本，称为交互算法，它提供了Hadamard和Walsh变换的有效计算。Yates的算法仍然被用于统计设计和实验分析领域。

1942年，G.C.Danielson和CorneliusLanczos发表了他们的版本，用于计算X射线晶体学的DFT，在这个领域，傅里叶变换的计算是一个可怕的瓶颈。

虽然过去的许多方法都集中在减少恒定系数的在利用对称性进行计算的过程中，丹尼尔森和兰佐斯意识到，可以利用周期性并应用加倍的技巧，使[N]增加一倍，而劳动量仅略高于一倍，不过和高斯一样，他们并没有分析出这导致了JamesCooley和JohnTukey独立地重新发现了这些早期的算法，并在1965年发表了一个更通用的FFT，当N是复合的而不一定是2的幂时，也适用，同时还分析了缩放。

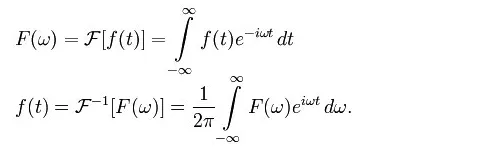
Tukey是在肯尼迪总统的科学咨询委员会的一次会议上提出这个想法的，当时的讨论主题是通过设置传感器从外部包围苏联来检测苏联的核试验。为了分析这些传感器的输出，将需要一种FFT算法。

在与Tukey的讨论中，RichardGarwin认识到该算法的普遍适用性，不仅适用于国家安全问题，也适用于广泛的问题，包括他直接感兴趣的一个问题，即确定氦-3的三维晶体中自旋方向的周期性。加文将图基的想法交给库利（两人都在IBM的沃森实验室工作）进行实施。

Cooley和Tukey在相对较短的6个月内发表了论文。由于Tukey不在IBM工作，这一想法的专利性受到怀疑，该算法进入了公共领域，而这一领域经历了2000年的计算xxx。