混淆矩阵

在机器学习领域，特别是统计分类问题，混淆矩阵，也被称为误差矩阵，是一个特定的表格布局，允许可视化算法的性能，通常是监督学习的算法。矩阵的每一行代表实际类中的实例，而每一列代表预测类中的实例，反之亦然--这两种变体都可以在文献中找到。这个名字源于这样一个事实：它使人们很容易看到系统是否混淆了两个类。它是一种特殊的或然率表，有两个维度（实际和预测），在这两个维度上有相同的类集。

给出一个12人的样本，其中8人被诊断为癌症，4人没有患癌症，患癌症的人属于1类（阳性），非癌症的人属于0类（阴性），我们可以将这些数据显示如下。假设我们有一个分类器，能以某种方式区分患癌和不患癌的个体，我们可以把这12个个体通过分类器来运行它们。然后，分类器做出了9个准确的预测，遗漏了3个：2个患有癌症的人被错误地预测为没有癌症（样本1和2），1个没有癌症的人被错误地预测为患有癌症（样本9）。请注意，如果我们将实际分类集与预测分类集进行比较，在任何特定的列中都可能产生4种不同的结果。一，如果实际分类是阳性，预测分类是阳性（1,1），这被称为真阳性结果，因为阳性样本被分类器正确识别。二，如果实际分类是阳性而预测分类是阴性（1,0），这被称为假阴性结果，因为阳性样本被分类器错误地识别为阴性。第三，如果实际分类是阴性，而预测分类是阳性（0,1），这被称为假阳性结果，因为阴性样本被分类器错误地识别为阳性。第四，如果实际分类是负面的，而预测分类是负面的（0,0），这被称为真正的负面结果，因为负面样本被分类器正确识别。然后，我们可以进行实际分类和预测分类之间的比较，并将这一信息添加到表格中，使正确的结果显示为绿色，这样它们就更容易被识别。

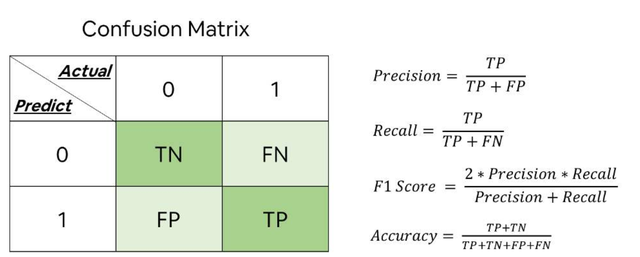
任何二元混淆矩阵的模板都使用上面讨论的四种结果（真阳性、假阴性、假阳性和真阴性）以及阳性和阴性分类。这四种结果可以用一个2×2的混淆矩阵来表述。上面三个数据表的颜色惯例被选为与这个混淆矩阵相匹配，以便于区分数据。现在，我们可以简单地将每一种类型的结果累加起来，代入模板，形成一个混淆矩阵，简明地总结出测试分类器的结果。在这个混淆矩阵中，在8个有癌症的样本中，系统判断出2个没有癌症，而在4个没有癌症的样本中，它预测出1个确实有癌症。所有正确的预测都位于表格的对角线上（用绿色突出显示），因此很容易目测到表格中的预测错误，因为对角线以外的值将代表这些错误。通过将混淆矩阵的两行相加，也可以推算出原始数据集中的阳性（P）和阴性（N）样本的总数。

在预测分析中，混淆表（有时也称为混淆矩阵）是一个有两行和两列的表格，报告真阳性、假阴性、假阳性和真阴性的数量。这比简单地观察正确分类的比例（准确率）可以进行更详细的分析。如果数据集是不平衡的，也就是说，当不同类别的观察结果数量相差很大时，准确率将产生误导性结果。