早期停止

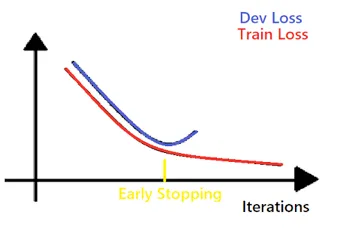
在机器学习中，早期停止是一种正则化的形式，用于避免在用梯度下降等迭代方法训练学习者时出现过度拟合。这种方法更新学习者，使其在每次迭代中更好地适应训练数据。在一定程度上，这可以提高学习者在训练集之外的数据上的表现。然而，过了这个点，提高学习者对训练数据的拟合度是以增加泛化误差为代价的。早期停止规则为学习者在开始过度拟合之前可以运行多少次迭代提供指导。早期停止规则已被用于许多不同的机器学习方法中，并具有不同的理论基础。

本节介绍了描述早期停止方法所需的一些基本机器学习概念。

机器学习算法基于有限的训练数据集来训练一个模型。在这个训练过程中，模型的评估是基于它对训练集中的观察结果的预测程度。然而，一般来说，机器学习方案的目标是产生一个具有普适性的模型，也就是说，预测以前未见过的观察。当一个模型很好地适合训练集中的数据，同时产生较大的泛化误差时，就会出现过拟合。

在机器学习的背景下，正则化是指修改学习算法的过程，以防止过度拟合。这种平滑性可以通过固定模型中的参数数量来明确实施，也可以通过增加成本函数来实施，如Tikhonov正则化。Tikhonov正则化，以及主成分回归和许多其他正则化方案，都属于谱系正则化的范畴，正则化的特点是应用滤波器。早期止损也属于这一类方法。

梯度下降法是一阶、迭代、优化方法。每次迭代都是通过在目标函数梯度的负值方向迈出一步来更新优化问题的近似解。通过适当地选择步长，这种方法可以收敛到目标函数的局部最小值。梯度下降法在机器学习中的应用是定义一个反映学习者在训练集上的误差的损失函数，然后使该函数最小化。

统计学习理论中的早期停止早期停止可以用来规范机器学习中遇到的非参数回归问题。对于一个给定的输入空间。{displaystyleZ=XtimesY}，这类问题的目标是近似回归函数。，这类问题的目标是对回归函数进行近似。近似回归函数的一个常见选择是使用再现核希尔伯特空间的函数。这些空间可以是无限维的，其中它们可以提供过度拟合任意大小的训练集的解决方案。因此，正则化对这些方法特别重要。

对非参数回归问题进行规范化的一种方法是对梯度下降等迭代程序应用早期停止规则。为这些问题提出的早期停止规则是基于对作为迭代次数函数的泛化误差的上限分析。它们产生了可以在开始求解过程之前计算出的运行迭代次数的处方。例子。最小二乘法损失(改编自Yao,RosascoandCaponnetto,2007){displaystylef}是重现系数的成员。是再现核希尔伯特空间的一个成员{displaystyle{mathcal{H}}。.也就是说，最小化一个最小二乘损失函数的预期风险。由于{displaystyle{mathcal{E}}}取决于未知的概率度量。取决于未知的概率度量