希尔伯特-黄转换（HHT）是一种将信号与趋势一起分解为所谓的固有模式函数（IMF），并获得瞬时频率数据的方法。它被设计为对非平稳和非线性的数据有很好的效果。与其他常见的变换如傅里叶变换相比，HHT是一种可以应用于数据集的算法，而不是一种理论工具。

希尔伯特-黄转换（HHT）是NASA指定的名称，由Norden E. Huang等人提出（1996，1998，1999，2003，2012）。它是经验模式分解（EMD）和希尔伯特频谱分析（HSA）的结果。HHT使用EMD方法将信号分解为所谓的具有趋势的内在模式函数（IMF），并将HSA方法应用于IMF，以获得瞬时频率数据。由于信号是在时域分解的，而且IMF的长度与原始信号相同，所以HHT保留了变化频率的特征。这是HHT的一个重要优势，因为现实世界的信号通常有多个原因发生在不同的时间间隔。HHT提供了一种分析非平稳和非线性时间序列数据的新方法。

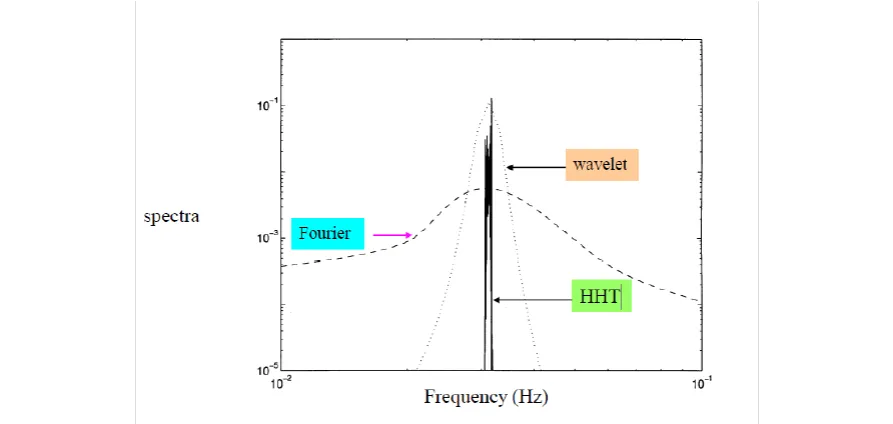
HHT的基本部分是经验模式分解（EMD）方法。将信号分解成各种成分，EMD可以与其他分析方法如傅里叶变换和小波变换进行比较。使用EMD方法，任何复杂的数据集都可以被分解成有限的、通常是少量的成分。这些成分构成了原始信号的一个完整的、近乎正交的基础。此外，它们可以被描述为内在的模式函数（IMF）。

因为第一个IMF通常带有最多振荡（高频）成分，它可以被拒绝以去除高频成分（如随机噪声）。基于EMD的平滑算法已被广泛用于地震数据处理，其中高质量的地震记录被高度要求。

在不离开时域的情况下，EMD是自适应的和高效的。由于分解是基于数据的局部特征时间尺度，它可以应用于非线性和非平稳过程。

本征模式函数（IMF）被定义为满足以下要求的函数：

• 在整个数据集中，极值的数量和零交叉的数量必须相等或最多相差1。
• 在任何一点上，由局部最大值定义的包络和由局部最小值定义的包络的平均值为零。

它代表一个一般的简单振荡模式，作为简单谐波函数的对应物。根据定义，国际货币基金组织是任何具有相同数量极值和零交叉点的函数，其包络是关于零的对称性。这个定义保证了IMF有一个良好的希尔伯特变换。

希尔伯特频谱分析（HSA）是一种将每个IMF的瞬时频率作为时间函数来研究的方法。最后的结果是信号振幅（或能量）的频率-时间分布，指定为希尔伯特频谱，它允许识别局部特征。

内在模式函数（IMF）的振幅和频率可以随时间变化，它必须满足以下规则：

• 极端数（局部最大&amp；局部最小）和零交叉数必须相等或最多相差1。
• 在任何一点上，由局部最大值定义的包络和由局部最小值定义的包络的平均值都接近于零。

经验模式分解（EMD）方法是将任何给定的数据简化为内在模式函数（IMF）集合的必要步骤，希尔伯特谱分析可以应用于此。

IMF代表简单的振荡模式，作为简单谐波函数的对应物，但它更普遍：IMF可以沿时间轴具有可变的振幅和频率，而不是简单谐波成分中的恒定振幅和频率。

提取IMF的过程被称为筛分。筛选过程如下：

• 识别测试数据中的所有局部极值。
• 用一条立方样条线连接所有的局部极值，作为上包络。
• 重复局部极值的程序，产生下包络。

上包络和下包络应该涵盖它们之间的所有数据。它们的平均值是m1。数据和m1之间的差异是第一部分h1。

X ( t ) – m 1 = h 1 。{dISPlaystyle X(t)-m_{1}=h_{1}.,}

理想情况下，h1应该满足IMF的定义，因为上述h1的构造应该使其成为对称的，并且所有最大值为正，所有最小值为负。