后缀数组

在计算机科学中，后缀数组是一个字符串的所有后缀的排序数组。它是一种用于全文索引、数据压缩算法和文献计量学等领域的数据结构。

增强型后缀数组 (ESA) 是带有附加表的后缀数组，这些表重现后缀树的全部功能，同时保持相同的时间和内存复杂度。字符串所有后缀的子集的后缀数组称为稀疏后缀数组。 已经开发了多种概率算法来最小化额外的内存使用，包括最佳时间和内存算法。

让 S = S [1] S [2]。 . . S [ n ] {displaystyle S=S[1]S[2]...S[n]} 是一个 n {textstyle n} -string 并且让 S [ i , j ] {displaystyle S [i,j]} 表示 S {displaystyle S} 的子串，范围从 i {displaystyle i} 到 j {displaystyle j} 包括在内。

S {displaystyle S} 的后缀数组 A {displaystyle A} 现在被定义为一个整数数组，提供按字典顺序排列的 S {displaystyle S} 后缀的起始位置。 这意味着，条目 A [ i ] {displaystyle A[i]} 包含第 i {displaystyle i} 的起始位置 - S {displaystyle S} 中的xxx个最小后缀，因此对于所有 1 ≤ i ≤ n {displaystyle 1leq ileq n} : S [ A [ i − 1 ] , n ] <; S [ A [ i ] , n ] {displaystyle S[A[i-1],n]<S[A[i],n]} 。

S {displaystyle S} 的每个后缀在 A {displaystyle A} 中只出现一次。 后缀是简单的字符串。 这些字符串在它们的起始位置（整数索引）保存在 A {displaystyle A} 之前被排序（就像在纸质字典中一样）。

考虑文本 S {displaystyle S} =banana$ 被索引：

文本以特殊标记字母 $ 结尾，它是xxx的，并且在字典序上比任何其他字符都小。 文本具有以下后缀：

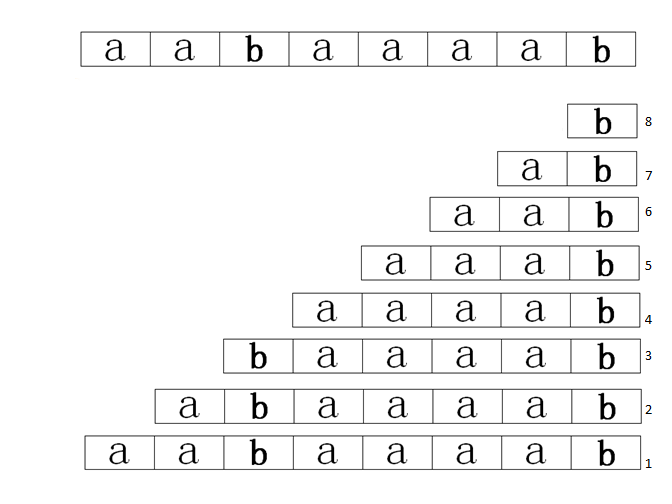
这些后缀可以按升序排序：

后缀数组 A {displaystyle A} 包含这些排序后缀的起始位置：

为清楚起见，后缀数组在下方垂直写出：

因此，例如， A [ 3 ] {displaystyle A[3]} 包含值 4，因此指的是 S {displaystyle S} 中从位置 4 开始的后缀，即后缀 ana$。

后缀数组与后缀树密切相关：

• 后缀数组可以通过执行后缀树的深度优先遍历来构造。 后缀数组对应于在遍历期间按访问顺序给出的叶标签，如果边是按其xxx个字符的字典顺序访问的。
• 通过使用后缀数组和LCP 数组的组合，可以在线性时间内构造后缀树。 有关算法的说明，请参阅 LCP 阵列文章中的相应部分。

已经表明，每个后缀树算法都可以系统地替换为使用使用附加信息增强的后缀数组（例如 LCP 数组）的算法，并以相同的时间复杂度解决相同的问题。后缀数组相对于后缀树的优势 包括改进的空间要求、更简单的线性时间构造算法（例如，与 Ukkonen 的算法相比）和改进的缓存局部性。

后缩数字组由 Manber & 介绍 Myers (1990) 为了改进后缀树的空间需求：后缩数组存储 n {displaystyle n} 整数。假设一个整数需要 4 {displaystyle 4} 字节，一个后缀数组总共需要 4 n {displaystyle 4n} 字节。这明显少于谨慎的后缀树实现所需的 20 n {displaystyle 20n} 字节。

然而，在某些应用程序中，后缀数组的空间要求可能仍然过高。按位分析，后缀数组需要 O ( n log ⁡ n ) {displaystyle {mathcal {O}}(nlog n)} 空间，而原始文本在大小为 σ { displaystyle sigma } 只需要 O ( n log ⁡ σ ) {displaystyle {mathcal {O}}(nlog sigma )} 位。对于 σ = 4 {displaystyle sigma =4} 和 n = 3.4 × 10 9 {displaystyle n=3.4times 10{9}} 因此，后缀数组占用的内存比基因组本身多16倍。