简介
编辑挠度在结构工程中,挠度是结构元件的一部分在负载下位移的程度(因为它变形)。 它可以指角度或距离。
构件在载荷下的偏转距离可以通过对以数学方式描述构件在该载荷下偏转形状的斜率的函数进行积分来计算。
对于普通梁配置的挠度和离散位置的负载情况,存在标准公式。否则,使用虚功、直接积分、Castigliano 方法、Macaulay 方法或直接刚度方法等方法。 梁单元的挠度通常根据欧拉-伯努利梁方程计算,而板或壳单元的挠度则使用板或壳理论计算。
在这种情况下使用挠度的一个例子是建筑施工。 建筑师和工程师为各种应用选择材料。
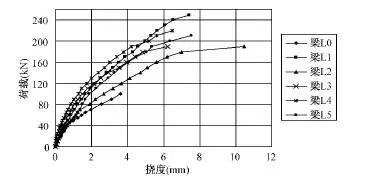
各种载荷和支撑的梁偏转
编辑梁的几何形状和成分可能有很大差异。 例如,梁可以是直的或弯曲的。 它的横截面可以是恒定的,也可以是锥形的。 它可能完全由相同的材料制成(均质),也可能由不同的材料组成(复合材料)。 其中一些事情使分析变得困难,但许多工程应用程序涉及的情况并不那么复杂。 如果出现以下情况,分析将得到简化:
在这种情况下,控制光束偏转的方程式 ( w {dISPlaystyle w} ) 可以近似为:
d 2 w ( x ) d x 2 = M ( x ) E ( x ) I ( x ) {diSPlaystyle {cfrac {mathrm {d} {2}w(x)}{mathrm {d } x{2}}}={frac {M(x)}{E(x)I(x)}}}
其中偏转形状相对于 x {displaystyle x} 的二阶导数(x {displaystyle x} 是沿光束长度的水平位置)被解释为其曲率,E {displaystyle E} 是杨氏模量,I {displaystyle I} 是横截面的面积惯性矩,M {displaystyle M} 是梁的内部弯矩。
此外,如果梁不是锥形的并且是均匀的,并且受到分布载荷 q {displaystyle q} 的作用,则上面的表达式可以写成:
E I d 4 w ( x ) d x 4 = q ( x ) {displaystyle EI~{cfrac {mathrm {d} {4}w(x)}{mathrm {d} x{4} }}=q(x)}
该方程可以求解各种载荷和边界条件。 下面显示了一些简单的例子。 所表达的公式是为具有小挠度和线性弹性特性的细长、均匀、棱柱形梁开发的近似值。 在这些限制下,近似值的结果应在实际偏转的 5% 以内。
悬臂梁
编辑悬臂梁的一端是固定的,因此该端的斜率和挠度必须为零。
端载悬臂梁
示例图像中自由端的弹性偏转 δ {displaystyle delta } 和偏转角 ϕ {displaystyle phi }(以弧度为单位):一个(失重)悬臂梁,具有端部载荷
均布悬臂梁
悬臂梁在均匀载荷下的自由端 B 处的挠度
q {displaystyle q} = 梁上的均匀载荷(每单位长度的力)L {displaystyle L} = 梁的长度 E {displaystyle E} = 弹性模量 I {displaystyle I} = 面积力矩 截面惯性
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/207087/
