相空间

在动力系统理论中，相空间是表示系统所有可能状态的空间，每个可能状态对应于相空间中的一个唯 一点。对于机械系统，相空间通常由位置和动量变量的所有可能值组成。它是直接空间和倒易空间的外积。

相空间的概念是在 19 世纪后期由路德维希·玻尔兹曼、亨利·庞加莱和约西亚·威拉德·吉布斯提出的。

在相空间中，系统的每个自由度或参数都表示为多维空间的轴； 一维系统称为相线，而二维系统称为相平面。对于系统的每种可能状态或系统参数值的允许组合，多维空间中都包含一个点。系统随时间演化的状态通过高维空间追踪一条路径（系统的相空间轨迹）。

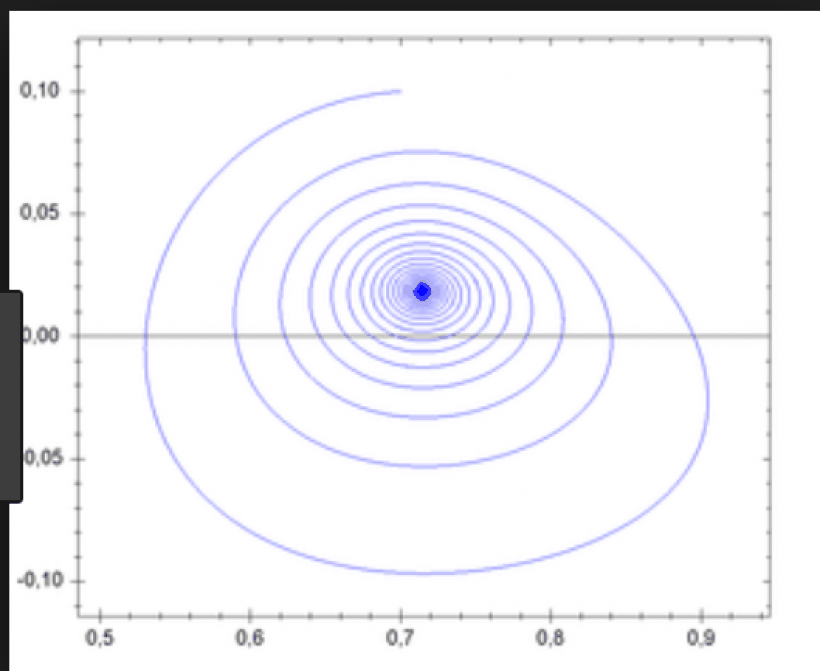
相空间轨迹表示与从一个特定初始条件开始兼容的状态集，位于表示与从任何初始条件开始兼容的状态集的完整相空间中。作为一个整体，相图代表了系统的所有可能，它的形状可以很容易地阐明系统的品质，否则这些品质可能不明显。

相空间可能包含大量维度。 例如，包含许多分子的气体可能需要每个粒子的 x、y 和 z 位置和动量的单独维度（理想化单原子气体的 6 个维度），并且对于更复杂的分子系统，需要额外的维度来描述振动模式 的分子键，以及围绕 3 个轴旋转。

在分析仅限于围绕和沿各种旋转或平移轴运动的机械系统的行为时，相空间更容易使用 - 例如 在机器人技术中，例如分析机械臂的运动范围或确定实现特定位置/动量结果的最佳路径。

在经典力学中，任何选择广义坐标 qi 的位置（即配置空间上的坐标）定义共轭广义动量 pi，它们一起定义相空间上的坐标。

更抽象地说，在经典力学中，相空间是配置空间的余切丛，在这种解释中，上述过程表示配置空间上局部坐标的选择导致余切空间上标准辛结构的自然局部达布坐标的选择 .

经典统计力学研究了该空间中系统集合的运动。 这种系统中点的局部密度服从刘维尔定理，因此可以视为常数。