布朗运动

布朗运动或 pedesis（来自古希腊语：πήδησις /pɛ̌ːdɛːsis/ leaping）是悬浮在介质（液体或气体）中的粒子的随机运动。

这种运动模式通常包括粒子在流体子域内位置的随机波动，然后重新定位到另一个子域。 每次搬迁之后，新封闭体积内都会出现更多波动。 该模式描述了由给定温度定义的处于热平衡状态的流体。 在这样的流体中，不存在优先流动方向（如在运输现象中）。 更具体地说，流体的整体线性和角动量随时间保持为零。 分子布朗运动的动能，连同分子旋转和振动的动能，总结为流体内能的热量分量（均分定理）。

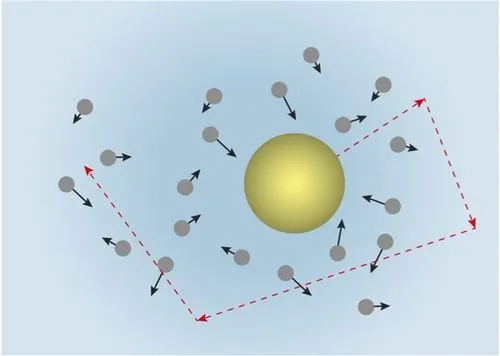
这种运动以植物学家罗伯特·布朗的名字命名，他于 1827 年首次描述了这一现象，当时他通过显微镜观察浸入水中的植物 Clarkia pulchella 的花粉。 大约八十年后的 1905 年，理论物理学家阿尔伯特·爱因斯坦发表了一篇论文，他将花粉颗粒的运动模拟为被单个水分子移动，这是他的xxx个重大科学贡献之一。 原子轰击力的方向不断变化，在不同时间，粒子在一侧受到的撞击比另一侧更多，导致运动看似随机。 这种对布朗运动的解释成为原子和分子存在的有力证据，并在 1908 年由让·佩兰通过实验进一步验证。佩兰因在物质的不连续结构方面的工作而获得 1926 年的诺贝尔物理学奖。

产生布朗模式的多体相互作用无法通过考虑每个相关分子的模型来解决。 因此，只能使用应用于分子群体的概率模型来描述它。 下面介绍了爱因斯坦和 Smoluchowski 的两个这样的统计力学模型。 另一个纯概率模型类是随机过程模型类。 存在收敛于（在极限内）布朗运动的更简单和更复杂的随机过程序列（参见随机游走和 Donsker 定理）。

罗马哲学家兼诗人卢克莱修的科学诗论事物的本质（公元前 60 年）在第二卷的第 113-140 节中对尘埃粒子的运动进行了非凡的描述。 他用这个作为原子存在的证明：

观察当阳光进入建筑物并照亮其阴暗处时会发生什么。 你会看到许多微小的粒子以多种方式混合......它们的舞蹈是我们看不见的物质潜在运动的实际指示......它起源于自身移动的原子[即自发地 ]. 然后，那些从原子的推动力中移除最少的小复合体在它们无形的打击的影响下开始运动，进而对稍大的物体开炮。 因此，运动从原子开始，逐渐浮现到我们的感官层面，以至于那些物体在运动，我们在阳光下看到，被看不见的打击所推动。

虽然尘埃颗粒的混合、翻滚运动主要是由气流引起的，但小尘埃颗粒的闪闪发光、摇晃的运动主要是由真正的布朗动力学引起的； 卢克莱修用一个错误的例子完美地描述和解释了布朗运动。

虽然 Jan Ingenhousz 在 1785 年描述了煤尘颗粒在酒精表面的不规则运动，但这种现象的发现通常归功于 1827 年的植物学家罗伯特布朗。布朗正在研究悬浮在水中的植物 Clarkia pulchella 的花粉粒 当他观察到由花粉粒喷出的微小颗粒时，他在显微镜下进行了抖动运动。 通过用无机物粒子重复实验，他能够排除这种运动与生命有关的可能性，尽管其起源尚待解释。

Thorvald N. Thiele 是 Thorvald N. Thiele 在 1880 年发表的一篇关于最小二乘法的论文中，xxx个描述布朗运动背后的数学的人。

随后 Louis Bachelier 在 1900 年的博士论文 The theory of speculation 中独立跟进，他在其中提出 股票和期权市场的随机分析。 股票市场的布朗运动模型经常被引用，但 Benoit Mandelbrot 拒绝将其应用于股票价格变动，部分原因是这些是不连续的。

阿尔伯特·爱因斯坦（在他 1905 年的一篇论文中）和玛丽安·斯莫卢霍夫斯基（Marian Smoluchowski，1906 年）将这个问题的解决方案引起了物理学家的注意，并将其作为一种间接证实原子和分子存在的方法。