米-门二氏动力学

在生物化学中，米-门二氏动力学是最著名的酶动力学模型之一。 它以德国生物化学家 Leonor Michaelis 和加拿大医生 Maud Menten 的名字命名。 该模型采用描述酶促反应速率的方程式形式，通过关联反应速率 v {\displaystyle v}（产物形成速率，[ P ] {\displaystyle [{\ce {P}}] } ) 到 [ S ] {\displaystyle [{\ce {S}}]} ，底物 S 的浓度。

这个方程称为 Michaelis-Menten 方程。 这里，V max {\displaystyle V_{\max }} 表示系统达到的xxx速率，发生在给定酶浓度的饱和底物浓度下。 当米氏常数 K M {\displaystyle K_{\mathrm {M} }} 在数值上等于底物浓度时，反应速率是 V max {\displaystyle V_{\max }} 的一半 . 通常假设涉及单一底物的生化反应遵循米-门二氏动力学，而不考虑模型的基本假设。

1901 年，法国物理化学家 Victor Henri 发现酶反应是由酶和底物之间的键（更一般地，结合相互作用）引发的。 德国生物化学家 Leonor Michaelis 和加拿大医生 Maud Menten 接手了他的工作，他们研究了一种酶促反应机制的动力学，转化酶催化蔗糖水解成葡萄糖和果糖。 1913年，他们提出了反应的数学模型。 它涉及酶 E 与底物 S 结合形成复合物 ES，后者又释放产物 P，使原始酶再生。

其中 k f {\displaystyle k_{f}}（正向速率常数），k r {\displaystyle k_{r}}（反向速率常数），以及 k c a t {\displaystyle k_{\mathrm {cat} }}（ 催化速率常数）表示速率常数，S（底物）和 ES（酶-底物复合物）之间的双箭头表示酶-底物结合是一个可逆过程，单向前箭头表示 P（产物 ).

在某些假设下——例如酶浓度远低于底物浓度

反应顺序取决于分母中两项的相对大小。

当所有酶都与底物结合时达到该速率。 k c a t {\displaystyle k_{\mathrm {cat} }} ，周转数，是每秒每个酶分子转化为产物的底物分子的xxx数量。 进一步添加底物不会增加据说饱和的速率。

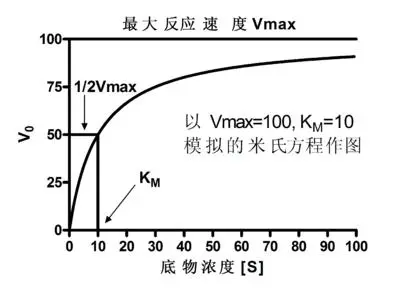
米氏常数 K M {\displaystyle K_{\mathrm {M} }} 的值在数值上等于反应速率为 [ S ] {\displaystyle {\ce {[S]}}} 在半xxx值处，并且是底物对酶的亲和力的量度——小的 K M {\displaystyle K_{\mathrm {M} }} 表示高亲和力，这意味着速率将接近 V max { \displaystyle V_{\max }} 具有较低的 [ S ] {\displaystyle {\ce {[S]}}} 而不是具有较大 K M {\displaystyle K_{\mathrm {M} } } 。 该常数不受酶浓度或纯度的影响。 K M {\displaystyle K_{\mathrm {M} }} 的值取决于酶和底物的特性，以及温度和 pH 等条件。