博欣内斯克方程

在流体动力学中，水波的 近似是对弱非线性和相当长的波浪有效的近似。

水波的 近似考虑了水平和垂直流速的垂直结构。 这导致非线性偏微分方程，称为 Boussinesq 型方程，其中包含频率色散（与不具有频率色散的浅水方程相反）。

虽然 Boussinesq 近似适用于相当长的波——即当波长与水深相比较大时——Stokes 展开更适用于短波（当波长与水深处于同一数量级或更短时） ).

Boussinesq 近似的基本思想是从流动方程中消除垂直坐标，同时保留水波下水流垂直结构的一些影响。 这很有用，因为波在水平面上传播并且在垂直方向上具有不同的（不是波状的）行为。

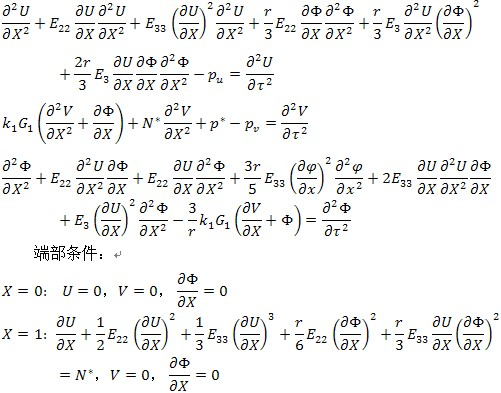
此后，将 Boussinesq 近似应用于剩余的流动方程，以消除对垂直坐标的依赖性。结果，得到的偏微分方程是水平坐标（和时间）的函数。

例如，考虑 (x,z) 平面中水平床上的势流，其中 x 是水平坐标，z 是垂直坐标。 床位于 z = -h，其中 h 是平均水深。

其中 φb(x,t) 是床层的速度势。 为 φ 调用拉普拉斯方程，对不可压缩流有效。