平面波

在物理学中，平面波是波或场的特例：一种物理量，其值在任何时刻在垂直于空间中固定方向的任何平面上都是恒定的。

对于空间中的任意位置 和任意时间 t，这样一个字段的值可以写成

F ( x → , t ) = G ( x → ⋅ n → , t )

其中 n → 是一个单位长度的向量，而 G ( d , t ) 是一个给出场的函数' s 值仅取决于两个实参数：时间 t 和标量值位移 d = x → ⋅ n → 。在垂直于 n → 的每个平面上，位移是恒定的。

字段 F 的值可以是标量、向量或任何其他物理或数学量。 它们可以是复数，如复指数平面波。

当 F {displaystyle F} 的值是向量时，如果向量总是与向量 n → 共线，则该波被称为纵波，并且 如果它们始终与其正交（垂直），则为横波。

平面波一词通常特指行进的平面波，其随时间的演变可以描述为场以恒定波速 c {displaystyle c} 沿垂直于波前的方向的简单平移。

其中 G ( u ) 现在是单个实参数 u = d − c t 的函数，它描述了波的轮廓，即值 场在时间 t = 0 ，对于每个位移 d = x → ⋅ n → 。 在这种情况下，n →被称为传播方向。 对于每个位移 d ，垂直于 n →的移动平面在距离原点 d + c t 处被称为 a 波前。 这个平面沿着传播方向 n → 以速度 c 行进； 并且场的值在它的每一点都是相同的，并且在时间上是恒定的。

该术语还用于，甚至更具体地，表示单色或正弦平面波：其轮廓 G ( u ) 是正弦函数的行进平面波。

参数 A 可以是标量或向量，称为波的振幅； 标量系数 f 是它的空间频率； 标量 φ 是它的相位。

真正的平面波不可能在物理上存在，因为它必须充满所有空间。 然而，平面波模型在物理学中很重要并被广泛使用。 当从与源的距离相比足够小的区域的任何部分观察时，由任何有限范围的源发射到大的均匀空间区域的波可以很好地近似为平面波。 例如，来自遥远恒星的光波到达望远镜就是这种情况。

驻波是一种场，其值可以表示为两个函数的乘积，一个仅取决于位置，另一个仅取决于时间。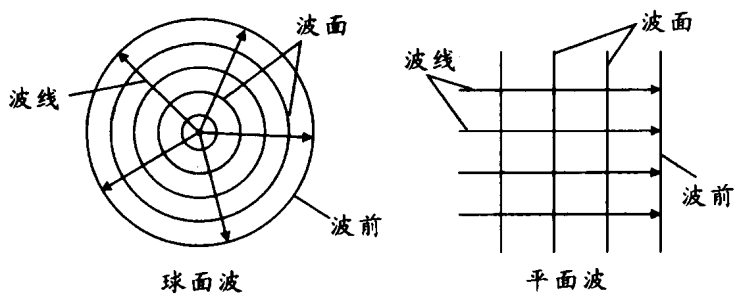

其中 G 是一个标量参数的函数具有标量或向量值，而 S是时间的标量函数。

这种表示不是xxx的，因为如果 S 和 G按倒数因子缩放，则会获得相同的字段值。 如果 | S ( 吨 ) 在感兴趣的时间间隔内有界，S 和 G 可以缩放，以便 | 的xxx值 S ( 吨 )是 1。