太阳系稳定性问题

太阳系的稳定性是天文学中很多研究的主题。 尽管这些行星在历史上一直是稳定的，并且在短期内也会如此，但它们之间的微弱引力效应可能会以不可预测的方式累积起来。

由于这个原因（除其他外），太阳系在数学混沌理论的技术意义上是混沌的，即使是太阳系轨道运动的最精确的长期模型也不会超过几千万。 年。

从人类的角度来看，太阳系是稳定的，而且远不止于此，因为在未来的几十亿年内，任何行星都不太可能相互碰撞或被逐出系统，而且地球的轨道将相对 稳定的。

自牛顿万有引力定律（1687 年）以来，数学家和天文学家（如皮埃尔-西蒙拉普拉斯、约瑟夫路易斯拉格朗日、卡尔弗里德里希高斯、亨利庞加莱、安德烈柯尔莫哥洛夫、弗拉基米尔阿诺德和于尔根莫塞尔）一直在寻找证据证明 行星运动的稳定性，这一探索导致了许多数学发展和太阳系稳定性的几个连续证明。

行星的轨道对长期变化是开放的。 太阳系建模是物理学的 n 体问题的一个例子，除非通过数值模拟，否则该问题通常无法解决。

当任何两个周期具有简单的数值比时，就会发生轨道共振。 太阳系中物体最基本的周期是它的轨道周期，轨道共振遍及太阳系。 1867年，美国天文学家丹尼尔柯克伍德注意到小行星带中的小行星并不是随机分布的。 在与木星共振对应的位置，带中有明显的间隙。 例如，在 3:1 共振点（距离 2.5 AU（3.7 亿公里；2.3 亿英里））或 2:1 共振点 3.3 AU（4.9 亿公里；3.1 亿英里）处没有小行星。 这些现在被称为柯克伍德缺口。 一些小行星后来被发现在这些空隙中运行，但它们的轨道不稳定，最终会因与大行星近距离接触而脱离共振。

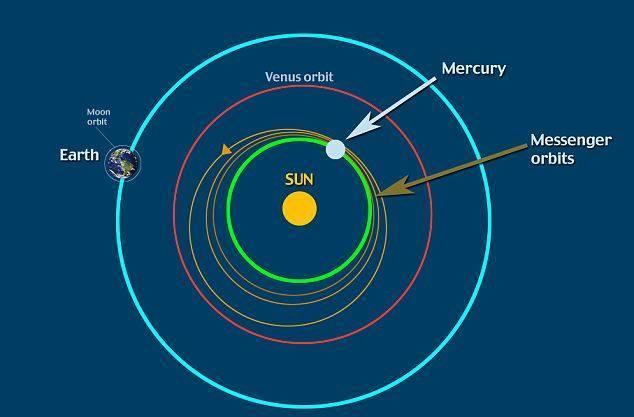
太阳系中另一种常见的共振形式是自旋轨道共振，其中自转周期（行星或月球绕其轴旋转一次所需的时间）与其轨道周期具有简单的数值关系。 一个例子是我们的月球，它处于 1:1 自旋轨道共振中，使其远离地球。 （此功能也称为潮汐锁定。）另一个例子是水星，它与太阳处于 3:2 自旋轨道共振。

行星的轨道在更长的时间尺度上是混乱的，以至于整个太阳系拥有 2-2.3 亿年范围内的李雅普诺夫时间。 在所有情况下，这意味着行星沿其轨道的位置最终变得无法准确预测。 在某些情况下，轨道本身可能会发生巨大变化。 这种混乱最强烈地表现为偏心率的变化，一些行星的轨道变得更椭圆或更椭圆。

在计算中，未知数包括小行星、太阳四极矩、太阳通过辐射和太阳风造成的质量损失、太阳风对行星磁层的阻力、银河潮汐力以及路过恒星的影响。

海王星-冥王星系统处于 3:2 轨道共振。 海军水面作战中心 DahLGren 分部的 C.J. Cohen 和 E.C. Hubbard 于 1965 年发现了这一点。虽然共振本身在短期内会保持稳定，但不可能以任何准确度预测冥王星的位置，因为 位置随着每个李雅普诺夫时间增长一个因子 e，对于冥王星来说，这是未来 10-2000 万年。因此，在数亿年的时间尺度上，冥王星的轨道相位变得无法确定，即使冥王星 的轨道在 10 MYR 时间尺度上似乎非常稳定（Ito 和 Tanikawa 2002，MNRAS）。

木星的卫星 Io 的轨道周期为 1.769 天，几乎是下一颗卫星 Europa（3.551 天）的一半。 它们处于 2:1 轨道共振。 这种特殊的共振具有重要的后果，因为木卫二的引力扰动了艾奥的轨道。 当 Io 靠近木星然后在轨道上远离木星时，它会经历显着的潮汐压力，从而导致活火山。 欧罗巴也与下一颗卫星木卫三处于 2:1 的共振状态。

由于一个小小的天体巧合，水星特别容易受到木星的影响：水星的近日点，即它最接近太阳的点，以一定的速度进动。