光学涡旋

光学涡旋（也称为光子量子涡旋、螺旋位错或相位奇点）是光场的零点； 零强度点。 该术语还用于描述其中具有这样一个零的光束。 对这些现象的研究被称为奇异光学。

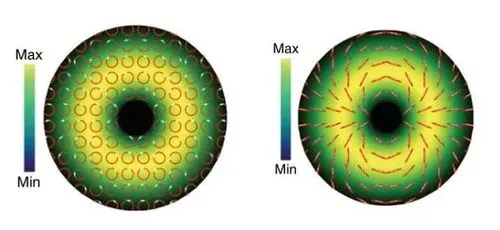
在光学涡旋中，光像开瓶器一样围绕其行进轴扭曲。 由于扭曲，轴上的光波本身相互抵消。 当投影到平面上时，光学涡旋看起来像一个光环，中间有一个黑洞。 根据光在一个波长中发生的扭曲次数，涡旋被赋予一个数字，称为拓扑电荷。 该数字始终是一个整数，可以是正数或负数，具体取决于扭曲的方向。 扭曲数越高，光绕轴旋转的速度越快。

这种旋转携带波列的轨道角动量，并将在电偶极子上引起扭矩。 轨道角动量不同于更常见的自旋角动量，它会产生圆极化。 在被捕获粒子的轨道运动中可以观察到光的轨道角动量。 用光的平面波干涉光学涡旋揭示了同心螺旋的螺旋相位。 螺旋中的臂数等于拓扑电荷。

通过在实验室中以各种方式创建光学涡旋来研究它们。 它们可以直接在激光中产生，或者可以使用多种方法中的任何一种将激光束扭曲成涡流，例如计算机生成的全息图、螺旋相位延迟结构或材料中的双折射涡流。

光学奇点是光场的零点。 场中的相位围绕这些零强度点循环（产生涡流这个名字）。 涡流是 2D 场中的点和 3D 场中的线（因为它们的余维为二）。 围绕包含涡流的路径对场的相位进行积分会产生 2π 的整数倍。 这个整数被称为涡流的拓扑电荷或强度。

超几何高斯模式 (HyGG) 在其中心有一个光学涡旋。 梁，具有以下形式

ψ ∝ e i m ϕ e − r 2 , {displaystyle psi propto e{imphi }e{-r{2}},!}

是由贝塞尔函数组成的近轴波动方程（参见近轴近似，实际方程见傅立叶光学文章）的解。 超几何高斯光束中的光子具有 mħ 的轨道角动量。 整数 m 也给出了光束中心的涡流强度。 圆偏振光的自旋角动量可以转化为轨道角动量。

有几种方法可以创建超几何高斯模式，包括螺旋相位板、计算机生成的全息图、模式转换、q 板或空间光调制器。

• 静态螺旋相位板或反射镜是螺旋形的晶体或塑料片，专为所需的拓扑电荷和入射波长而设计。 它们效率高，但价格昂贵。 可以通过在破裂的塑料片的两侧之间移动一个楔子来制作可调节的螺旋相位板。 离轴螺旋相位镜可用于高功率和超短激光器的模式转换。
• 计算机生成的全息图 (CGH) 是平面波和转移到胶片上的拉盖尔-高斯光束之间的计算干涉图。 CGH 类似于普通的 Ronchi 线性衍射光栅，除了叉位错。 入射激光束产生带有涡流的衍射图案，涡流的拓扑电荷随着衍射级数的增加而增加。 零级是高斯分布的，并且涡旋在此非衍射光束的两侧具有相反的螺旋性。 CGH 叉中的叉数与xxx衍射级涡旋的拓扑电荷直接相关。 可以点燃 CGH 以将更多强度引导至一阶。 漂白将其从强度光栅转变为相位光栅，从而提高效率。

• 模式转换需要 Hermite-Gaussian (HG) 模式，这可以很容易地在激光腔内或外部通过不太精确的方式进行。 一对散光透镜引入古伊相移，产生 LG 光束，其方位角和径向折射率取决于输入 HG。
• 空间光调制器是一种计算机控制的电子液晶设备，可以通过创建不同折射率的全息图来创建动态涡流、涡流阵列和其他类型的光束。 该全息图可能是叉形图案、螺旋相位板或具有非零拓扑电荷的类似图案。
• 由片段制成的可变形镜可用于动态地（以高达几千赫兹的速率）产生涡流，即使被 h 照亮