卡门涡街

在流体动力学中，卡门涡街（或 von 卡门涡街）是旋转涡流的重复模式，由称为涡流脱落的过程引起，它负责流体围绕钝体流动的不稳定分离。

可以使用不同的技术对 von 卡门涡街进行数学建模，包括但不限于使用 k-epsilon、SST、k-omega 和雷诺应力以及大涡模拟 (LES) 湍流模型求解完整的 Navier-Stokes 方程，通过 数值求解一些动态方程。

涡街将仅在特定的流速范围内形成，该范围由雷诺数 (Re) 的范围指定，通常高于约 90 的 Re 极限值。流动的（全局）雷诺数是比率的量度 围绕物体或通道的流体流动中的惯性力与粘性力的关系，可以定义为整个流体流动的全局速度的无量纲参数

U {\displaystyle U} = 自由流速度（即远离流体边界的流速 U ∞ {\displaystyle U_{\infty }} 就像身体相对于静止流体的速度， 或非粘性流速，通过伯努利方程计算），这是原始的全局流动参数，即要无量纲化的目标。

对于普通流动（通常可以认为是不可压缩或等温的流动），运动粘度在整个流场上处处均匀且随时间恒定，因此粘度参数无法选择，自然成为运动粘度 在所考虑的温度下所考虑的流体。 另一方面，参考长度始终是任意参数，因此在比较不同障碍物周围或不同形状通道中的流动时应特别注意：全局雷诺数应参考相同的参考长度。 这实际上是机翼和通道流量数据的最精确来源指定雷诺数参考长度的原因。 参考长度可以根据要进行的分析而变化：对于具有圆形截面的物体，例如圆柱体或球体，通常选择直径； 对于机翼、通用非圆形圆柱体或钝体或旋转体（如机身或潜艇），通常是剖面弦或剖面厚度，或实际上是稳定设计输入的一些其他给定宽度； 对于流动通道，通常是流体围绕其流动的水力直径。

对于空气动力学剖面，参考长度取决于分析。 事实上，通常选择翼型弦作为参考长度，也用于机翼截面和薄型材的空气动力系数，其中主要目标是最大化升力系数或升力/阻力比（即像通常在薄翼型理论中一样，一个 将使用弦雷诺作为流速参数来比较不同的剖面）。 另一方面，对于整流罩和支柱，给定的参数通常是要流线型的内部结构的尺寸（为了简单起见，我们假设它是一个圆形截面的梁），主要目标是最小化阻力系数或阻力 /升力比。

因此，自然成为参考长度的主要设计参数是型材厚度（型材尺寸或垂直于流动方向的面积），而不是型材弦。

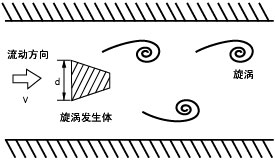
Re 值的范围随着涡流脱落的物体的大小和形状以及流体的运动粘度而变化。 对于圆柱体的尾流，其参考长度通常为圆柱体的直径 d，该范围的下限为 Re ≈ 47。涡流从圆边界的每一侧连续脱落，形成涡流行 在它的身后。 这种交替导致一排涡旋的核心与另一排两个涡旋核心之间的中点相对，从而产生了图中所示的独特图案。