阿佩尔方程

在经典力学中，阿佩尔方程是经典力学的替代一般公式。

Gibbs-Appell 方程为

Q r = ∂ S ∂ α r ,

其中 α r = q r 是任意广义加速度，或广义坐标的二阶时间导数 q r , Q r是对应的广义力。 广义力给出了完成的工作

d W = ∑ r = 1 D Q r d q r ,其中索引 r 运行在 D 广义坐标 q r 上，它通常对应于系统的自由度。 函数 S 被定义为粒子加速度平方的质量加权和，

S = 1 2 ∑ k = 1 N m k a k 2 ,

其中索引 k {displaystyle k} 遍历 K 粒子，并且

a k = r ¨ k = d 2 r k d t 2

是第 k 个粒子的加速度，是其位置向量 r k的二阶时间导数。 每个 r k 用广义坐标表示，而 a k 用广义加速度表示 .

阿佩尔的公式没有向经典力学引入任何新物理，因此等同于经典力学的其他重构，例如拉格朗日力学和哈密顿力学。 所有经典力学都包含在牛顿运动定律中。 在某些情况下，阿尔佩尔方法可能比常用的拉格朗日力学更方便，特别是涉及非完整约束时。 事实上，阿佩尔方程直接导出拉格朗日运动方程。 而且，它可以用来推导特别适合描述复杂航天器运动的凯恩方程。

对于 D 广义坐标中的无穷小变化，粒子位置 rk 的变化是

d r k = ∑ r = 1 D d q r ∂ r k ∂ q r

对时间取两个导数可得出加速度的等效方程

∂ a k ∂ α r = ∂ r k ∂ q r

广义坐标下的无穷小变化 dqr 所做的功为

d W = ∑ r = 1 D Q r d q r = ∑ k = 1 N F k ⋅ d r k = ∑ k = 1 N m k a k ⋅ d r k

其中第 k 个粒子的牛顿第二定律

F k = m k a k

已经用过。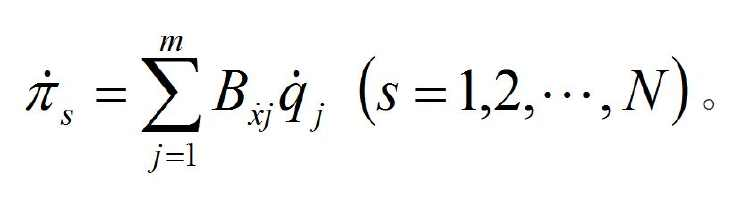

屈服阿尔佩尔方程

∂ S ∂ α r = Q r 。