波动方程

（双向）波动方程是一个二阶线性偏微分方程，用于描述波或驻波场——正如它们出现在经典物理学中——例如机械波（例如水波、声波和地震波）或 电磁波（包括光波）。 它出现在声学、电磁学和流体动力学等领域。 沿预定方向传播的单个机械波或电磁波也可以用一阶单向波动方程来描述，该方程更容易求解并且对非均匀介质也有效。

（双向）波动方程是描述波的二阶偏微分方程，包括行波和驻波； 后者可以被认为是沿相反方向传播的波的线性叠加。 本文主要关注通过一个时间变量t（代表时间的变量）和一个或多个空间变量x1的标量函数u = u (x1, x2, ..., xn; t)描述标量中的波的标量波动方程 , x2, ..., xn（表示所讨论空间中位置的变量），而有矢量波动方程描述矢量中的波，例如电场，磁场和磁矢量势和弹性波的波。 与矢量波动方程相比，标量波动方程可以看作是矢量波动方程的一个特例； 在笛卡尔坐标系中，标量波动方程是所考虑域中没有波源的矢量波的每个分量（对于每个坐标轴，例如x分量为x轴）所要满足的方程（ 即，空间和时间）。 例如在笛卡尔坐标系中，对于 ( E x , E y , E z ) {displaystyle (E_{x},E_{y},E_{z})} 作为电矢量场波的表示 E → {displaystyle {vec {E}}} 在没有波源的情况下，每个坐标轴分量 E i {displaystyle E_{i}} (i = x, y, or z) 必须满足 标量波动方程。 其他标量波动方程解 u 适用于标量中的物理量，例如液体或气体中的压力，或振动固体粒子沿某个特定方向远离其静止（平衡）位置的位移。

换一种说法：

• u 是表示相对于静止状态的位移的因素 - 它可以是气压高于或低于正常值，或者池塘中的水位高于或低于静止状态，或者其他。
• t代表时间。
• ∂ 2 u ∂ t 2 {displaystyle {frac {partial {2}u}{partial t{2}}}} 是位移如何加速的术语，即不是速度 位移变化的速度，但实际上位移速度本身变化的速度 - 它的加速度。
• x代表空间或位置。
• ∂ 2 u ∂ x 1 2 {displaystyle {frac {partial {2}u}{partial x_{1}{2}}}} 是位移如何变化的术语 在其中一个维度中的 x 点（如图形上的轴之一）。 它不是位移在空间中变化的速率，而是变化本身在空间中变化的速率——它的二重导数。 换句话说，这个术语表示位移的变化是如何在一个微小的周围区域中被挤压的。

该方程表明，在任何给定的情况下，在任何给定的点，位移加速的方式与位移变化在周围区域中被挤压的方式成正比。

或者用更简单的术语来说，位移被推动的方式与位移的尖锐程度成正比，反之亦然。

使用牛顿力学和矢量微积分的符号，波动方程可以更紧凑地写成

u ¨ = c 2 ∇ 2 u {displaystyle {ddot {u}}=c{2}nabla {2}u} .

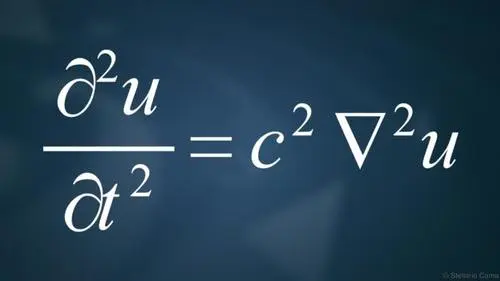
其中 u 上的双点 ¨ {displaystyle {ddot {u}}} 表示 u 的双时间导数，∇ 是 nabla 算子，而 ∇2 = ∇ · ∇ 是（空间）拉普拉斯算子（不是向量 拉普拉斯算子): u ¨ = ∂ 2 u ∂ t 2 ∇ = ( ∂ ∂ x 1 , ∂ ∂ x 2 , … , ∂ ∂ x n ) ∇ 2 = ∂ 2 ∂ x 1 2 + ∂ 2 ∂ x 2 2 + ⋯ + ∂ 2 ∂ x n 2 。