阿布拉罕-洛伦兹力
编辑在电磁物理学中,阿布拉罕-洛伦兹力(也称为洛伦兹-亚伯拉罕力)是加速带电粒子通过自相互作用发射电磁辐射引起的反冲力。 也称为辐射反作用力、辐射阻尼力或自力。 它以物理学家马克斯·亚伯拉罕和亨德里克·洛伦兹的名字命名。
该公式虽然早于狭义相对论,但最初是为非相对论速度近似计算的,后来被马克斯·亚伯拉罕扩展到任意速度,并被乔治·阿道夫·肖特证明在物理上是一致的。 非相对论形式称为洛伦兹自力,而相对论形式称为洛伦兹-狄拉克力或亚伯拉罕-洛伦兹-狄拉克力。 这些方程属于领域,而不是量子物理学领域,因此在大约康普顿波长或以下的距离上可能无效。 然而,有两个完全量子和相对论的公式类似物:一个称为亚伯拉罕-洛伦兹-狄拉克-朗之万方程,另一个是移动镜子上的自力。
力与物体电荷的平方乘以它所经历的加速度变化率(加速度的变化率)成正比。 力指向冲击的方向。 例如,在回旋加速器中,加加速度指向与速度相反的位置,辐射反应的方向与粒子的速度相反,从而提供制动作用。 阿布拉罕-洛伦兹力是无线电天线辐射无线电波的辐射电阻的来源。
亚伯拉罕-洛伦兹-狄拉克方程存在病态解,其中粒子在施加力之前加速,即所谓的预加速解。 由于这代表了一种先于其原因发生的结果(逆因果关系),一些理论推测该方程允许信号在时间上逆向传播,从而挑战了因果关系的物理原理。 Arthur D. Yaghjian 讨论了这个问题的一个解决方案,Fritz Rohrlich 和 Rodrigo Medina 进一步讨论了这个问题。
定义和描述
编辑在数学上,为非相对论速度近似 v ≪ c {dISPlaystyle vll c} 导出的洛伦兹自力以 SI 单位给出
或以高斯单位
F r a d = 2 3 q 2 c 3 a ˙ 。 {diSPlaystyle mathbf {F} _{mathrm {rad} }={2 over 3}{frac {q{2}}{c{3}}}mathbf { 刀塔}} 。}
其中 F r a d {displaystyle mathbf {F} _{mathrm {rad} }} 是力, a ˙ {displaystyle mathbf {dot {a}} } 是加速度的导数 ,或位移的三阶导数,也称为加加速度,μ0 是磁常数,ε0 是电常数,c 是自由空间中的光速,q 是粒子的电荷。
从物理上讲,加速电荷会发出辐射(根据拉莫尔公式),辐射会带走电荷的动量。 由于动量守恒,电荷被推向与发射辐射方向相反的方向。 事实上,上面辐射力的公式可以从拉莫尔公式推导出来,如下所示。
亚伯拉罕-洛伦兹力是洛伦兹自力对任意速度的概括
其中 γ 是与粒子速度 v 相关的洛伦兹因子。 该公式符合狭义相对论,简化为低速极限的洛伦兹自力表达式。
狄拉克推导出的任意形状基本电荷的辐射反应的协变形式被发现为:
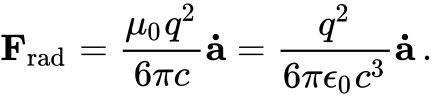
历史
编辑George FranCIS FitzGerald 于 1883 年首次计算了由电流引起的辐射电磁能,其中出现了辐射电阻。 然而,海因里希·赫兹 (Heinrich Hertz) 的偶极天线实验产生了更大的影响,并收集了庞加莱 (Poincaré) 对由于发射。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/221312/
