色散 (光学)

光的色散（dispersion of light）指的是复色光分解为单色光的现象；复色光通过棱镜分解成单色光的现象；光纤中由光源光谱成分中不同波长的不同群速度所引起的光脉冲展宽的现象。

在光学中，通过类比处理波传播的其他物理学分支，色散是一种波的相速度取决于其频率的现象；有时术语色散特别用于光学的特殊性。具有这种共同特性的介质可以称为色散介质（复数色散介质）。

尽管该术语在光学领域用于描述光和其他电磁波，但相同意义上的色散可以适用于任何类型的波动，例如声波和地震波以及重力波（海洋）中的声学色散 波浪）。在光学领域，色散是电信信号沿传输线（例如同轴电缆中的微波）或光纤中光脉冲的一种特性。在物理上，分散转化为通过吸收损失的动能。

在光学中，色散的一个重要且常见的结果是不同颜色光的折射角的变化，如色散棱镜产生的光谱和透镜的色差所示。 在很大程度上消除了色差的复合消色差透镜的设计中，使用了由其阿贝数 V 给出的玻璃色散的量化，其中较低的阿贝数对应于可见光谱中较大的色散。 在电信等一些应用中，波的绝 对相位通常并不重要，重要的只是波包或脉冲的传播； 在那种情况下，人们只对群速度随频率的变化感兴趣，即所谓的群速度色散。

所有常见传输介质的衰减（归一化为传输长度）也随频率变化，导致衰减失真； 这不是色散，尽管有时在紧密间隔的阻抗边界（例如电缆中的压接段）处的反射会产生信号失真，并进一步加剧信号带宽中观察到的不一致传输时间。

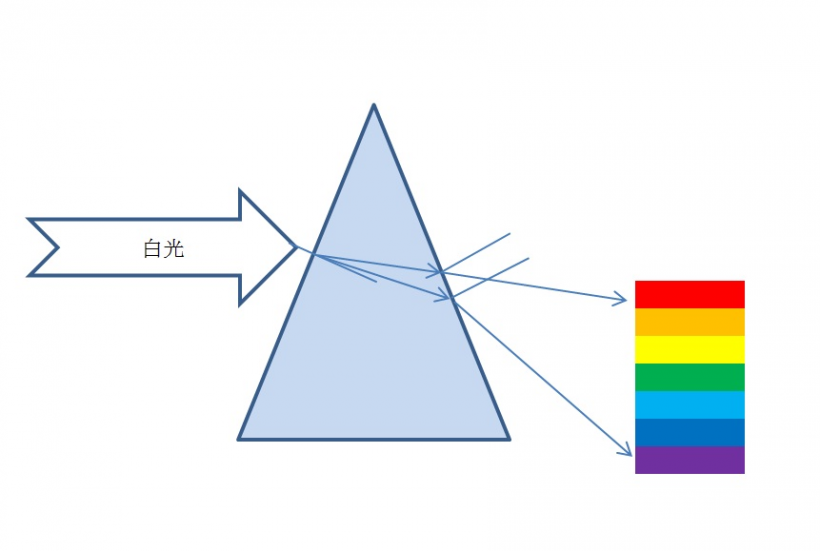
最熟悉的色散示例可能是彩虹，其中色散导致白光在空间上分离成不同波长（不同颜色）的分量。 然而，色散在许多其他情况下也会产生影响：例如，群速度色散会导致脉冲在光纤中传播，从而降低长距离信号的质量； 此外，群速度色散和非线性效应之间的抵消会导致孤子波。

大多数情况下，色散是指散装材料色散，即折射率随光频率的变化。 然而，在波导中也存在波导色散现象，在这种情况下，由于结构的几何形状，波在结构中的相速度仅取决于其频率。 更一般地，对于通过任何非均匀结构（例如，光子晶体）传播的波，无论波是否被限制在某个区域，都会发生波导色散。 在波导中，两种类型的色散通常都会存在，尽管它们不是严格的相加。 例如，在光纤中，材料和波导色散可以有效地相互抵消以产生零色散波长，这对于快速光纤通信很重要。

材料色散在光学应用中可能是理想的或不良的影响。 玻璃棱镜对光的色散用于构造光谱仪和光谱辐射计。 然而，在镜头中，色散会导致色差，这是一种可能降低显微镜、望远镜和摄影物镜图像质量的不良影响。

给定均匀介质中波的相速度 v 由下式给出

v = c n {displaystyle v={frac {c}{n}}}

其中 c 是光在真空中的速度，n 是介质的折射率。

通常，折射率是光的频率 f 的某种函数，因此 n = n(f)，或者相对于波的波长 n = n(λ)。 材料折射率对波长的依赖性通常通过其阿贝数或其在经验公式（例如 Cauchy 或 Sellmeier 方程）中的系数来量化。

由于 Kramers-Kronig 关系，折射率实部的波长依赖性与材料吸收有关，由折射率的虚部（也称为消光系数）描述。 特别地，对于非磁性材料（μ = μ0），Kramers-Kronig 关系中出现的磁化率 χ 是电磁化率 χe = n2 - 1。

光学中最常见的色散结果是通过棱镜将白光分离成色谱。