曲率

曲率（Curvature）是描述曲线弯曲程度的数值。它是弧长关于转角的变化率，在弧长相等时，转角越大，曲率值越大；转角相同时，弧长越小，曲率值越大。特别地，对于直线来说，曲率的数值为零；圆的曲率为其半径的倒数。

设曲线

的方程为

，其中

二阶可导。曲率

上取定一点

，点

处切线与

轴正向的夹角记为

。在点

附近，取

上另外一点

。曲线段

的弧长记为

，切线的转角记为

。曲线

在点

处的曲率

定义为当

越来越接近

时，弧长关于转角的变化率

。

曲率的概念起源于物理问题的研究。1673年，克里斯蒂安·惠更斯（Christian Huygens）在《钟表的振动》中，采用纯几何方法研究了平面曲线的性质。他在曲线上

点处给了一条固定的法线，当一条相邻的法线移向这固定的法线时，这两条法线的交点在固定法线上达到极限位置，就叫做曲线在

点的曲率中心。惠更斯证明了曲线上的点沿固定法线到这极限位置的距离是

，其长度是曲线在

点的曲率半径。牛顿（Newton）在《解析几何》中也引进了曲率中心的概念，作为

点的法线及其邻点法线的交点的极限点。牛顿还给出了曲率的公式，并计算了一些曲线，包括摆线在内的曲率。

克里斯蒂安·惠更斯

后来，曲率的不同定义方式被提出，有学者将概念进行了推广。1775年，欧拉（Euler）用参数方程表示空间曲线，他关于曲线的曲率半径的定义是

，其中

是曲线上相距

的两点的两个相邻切线的弧或角。之后，克莱劳特（Clairaut）曾经引进了空间曲线有两个曲率的想法：其中的一个曲率由欧拉叙述过的方式加以标准化；另一个曲率为现今的“挠率”——几何上表示一条曲线从

点处的一个平面离开的速率，后来由工程师和数学家米歇尔—昂热·兰克雷特（Michel-Ange Lancret）用分析方法求出。1826年，柯西（Cauchy）将曲率中心定义为两条无限接近曲线的法线的交点。次年，高斯（Gauss）在欧拉将曲率用于空间曲线和奥林德·罗德里格斯（Olinde Rodrigues）用于曲面的标形的基础上，对曲率进行了推广。高斯认识到曲面面积与球面上对应区域的面积之比的极限的重要性，并用它作为曲面在一点的曲率的定义。1854年，德国数学家波恩哈德·黎曼（Bernhard Riemann）在他的就职演说中，谈论了有关

维空间的曲率问题。

欧拉

曲率也可以定义为密切圆半径的倒数。曲率半径：设曲线

上点

处的曲率

，则

称为曲线在点

处的曲率半径，记为

，即

。曲率圆：作曲线在点

处切线的垂线（即法线），在曲线凹向一侧的法线上取

，以

为圆心，

为半径的圆称为曲线在点

处的曲率圆，

称为曲率中心。

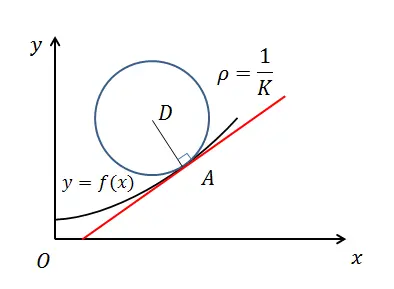曲率圆与曲率半径

曲率函数通过弧长参数化的方式来定义。在考虑机械手臂末端的三个手指如何移动并抓取物体时，设计者需要通过参数化路径来确保机械手臂能够准确地定位和调节手指。参数化路径不仅能够指导机械手臂到达正确的位置，还能正确地调整其手指的姿态。通过理解机械手臂沿着曲线移动时，三个手指与曲线的相对位置，可以进一步掌握曲线的几何特性，如曲线的旋转和平移。这种几何变换可以通过弗雷内特（Frenet）公式来描述。曲率函数：设

是有单位速度的曲线（

），以

表示

的单位切向量，

为

的法线。这里不要求

的长度为

，可以定义

的曲率函数为

。定义

为

的主法向量，定义

为

的副法向量，称

为

的弗雷内特标架。

、

、

沿曲线

的变化将反映曲线自身在空间中是如何旋转弯曲的。由

的定义知，

，所以曲率

描述了

方向上的变化。

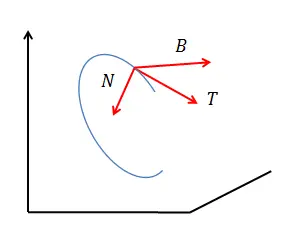曲线的弗雷内特标架

曲率梳：曲率梳是一种反映曲率分布的作图方式。定义直线段

，它表示在曲线上的某个点

，沿着法向量的方向画一条直线段。当

时，直线段的长度刚好等于曲率的绝对值。公式中，缩放因子

的作用是调整所有直线段的长度，避免出现太长的直线段而无法显示，或者因为所有曲率值都很接近于零而出现整体不明显的图形，经过相同比例的缩放后使直线段能够更合理且完美地呈现在曲线上。对曲线离散后，直线段就像一根根的“梳齿”一样挂在曲线上，外形看起来像梳子，并且梳齿的长短反映了曲率的变化规律。所以，这种将曲线和反映曲率值大小的直线段相结合的作图方式被形象地称为曲率梳。在曲率梳作图时，建议使用曲线的弧长参数化表示，这样能够使梳齿等距分布在曲线上，达到更好的视觉效果。

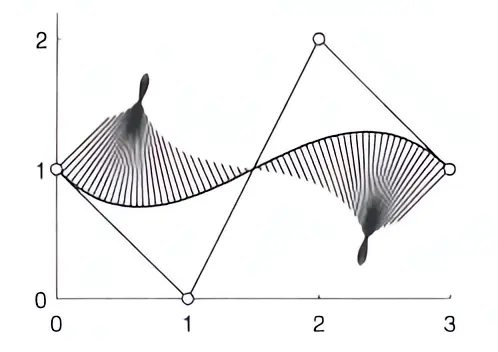曲率梳（d=0.8）

曲线的曲率是曲线切线倾角对弧长的变化率的xxx值。曲线在某一点的曲率刻画了曲线在该点的弯曲程度。当弧长相等的时候，转角越大，弯曲程度越大；当转角相同的时候，弧长越小，弯曲程度越大。对于直线来说，

，即直线不弯曲。对于圆来说，

，即圆弯曲程度处处相同，且半径越小，弯曲得越厉害。

曲率的几何意义

（1）普通方程：设曲线

的方程是

，且

存在，则曲线在

处的曲率公式为：

。（2）参数方程：设曲线

的参数方程为

，则曲线在点

处的曲率公式为：

。

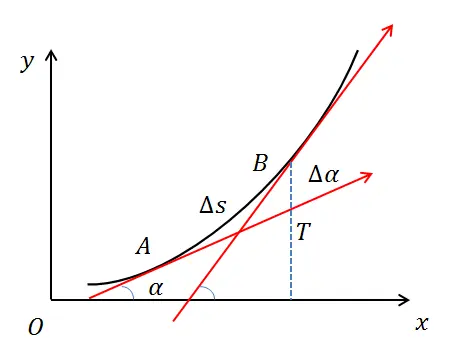曲率的计算公式示意图

证明：设平面曲线

具有二阶导数，此时

连续，曲线是光滑的。在曲线

上取两点

，

（

在

的右侧），记

的长为

，

的切线转角为

。由导数定义可知，

，即

，于是

，可得

，另外，当

很小时，有

，那么

，即

，由此可得弧微分

，将

和

代入曲率的定义式，可得到曲率的计算公式。（3）隐式方程：对于用隐式

定义的曲线，其相应的曲率公式是

，这里的下标

和

的意思是对

和

求偏导，例如

。

例1：抛物线

上哪一点的曲率xxx。解：由题意得

，

，

。可知，当

时，

xxx。又因

为抛物线的顶点，故抛物线在顶点处的曲率xxx。

例2：求摆线

在

处的曲率。解：由参数方程所确定的函数的求导法则，得

，上式两边再对

求一次导，得

，因此

。由曲率计算公式得

。

主曲率：经过曲面上一个点可以有无数个不同方向的曲线，因此曲面上的点在不同方向上有不同的曲率，主曲率为其中的xxx值和最小值，记作

和

。当曲线转向与平面给定法向量相同方向时，曲率取正值，否则取负值。主曲率方向互相垂直。高斯曲率与平均曲率：若已知曲面

上点

处的两个主曲率

和

，则定义高斯曲率为：

，定义平均曲率为：

。其中高斯曲率又称作全曲率或总曲率。第二基本形式：曲面的第二基本形式近似地等于曲面上一点

沿方向

的有向距离的两倍。它刻画了曲面在该点沿方向

上的弯曲程度。设曲面

有参数表示

，

，

为曲面的坐标切向量，这时

是

的单位法向量，曲面

的第二基本形式定义为

。将其进行参数化表示，可得到曲面的第二类基本量。曲面的高斯曲率和平均曲率可通过曲面的xxx、二类基本量来计算。曲面的形状算子：若

，则对

在

的每一切向量

，记

，其中

是

中

点邻域上的单位法向量场。

称为

在

点的由

导出的形状算子。

可以反映曲面的形状，其行列式、迹、特征值等都会代表一定的几何特征。曲面上点

处的高斯曲率

，平均曲率

。

黎曼曲率：对黎曼空间

内一点

的两个线性无关矢量

和

，

则为

，

所确定的平面的黎曼曲率，又称截面曲率。黎曼曲率是上述短程面在点

的高斯曲率。黎曼曲率

应具有如下的特点：（1）一般来说，

应与

、

有关。（2）在黎曼空间中，矢量的二次协变微商不可交换，实际上是由空间的弯曲所引起，可见

应与

有关。（3）

应为标量，则

应与坐标系无关。（4）当

、

线性组合成另外两个矢量

，

时，

、

所确定的切平面与

、

所确定的相同，因此

应是关于上述变换的不变量。（5）

为平直空间的充要条件是对全部矢量

、

都有

。

在工程学中，曲率可应用在预防滚动轴承损伤的理论中。通过计算滚动轴承内圈次表面裂纹的曲率，可以看出其对轴承的损伤程度以及寿命的影响。通过构建轴承有限元模型，模拟滚道次表面不同曲率的初始裂纹在径向载荷下的动态扩展过程，可以得出，在相同工况下，0.25mm~1.67mm曲率范围内的次表面裂纹，曲率较大的裂纹两端的应力较小；次表面裂纹的曲率越大，裂纹的扩展长度和角度均越小；曲率较大的次表面裂纹对轴承的损伤程度以及寿命的影响较小。这种机制的发现让工程师能够通过优化曲率来提高轴承的耐用性，通过调整次表面裂纹的曲率减少裂纹扩展对轴承性能的影响，延长其使用寿命。

滚动轴承

在物理学领域，重力梯度张量曲率广泛用于重力数据的处理和解释中。通过精确计算曲率的测量参考系以及考虑局部旋转的影响，重力梯度张量曲率的应用可以显著提升对重力数据边界识别的准确性。在该应用中，采用基于等位面的局部旋转坐标系是确保各种曲率准确计算的关键，这种方法有助于纠正以往在计算过程中可能出现的误差；在边界识别方面，使用局部坐标系下计算得到的高斯曲率，能够更有效地界定地下地质结构的边界。

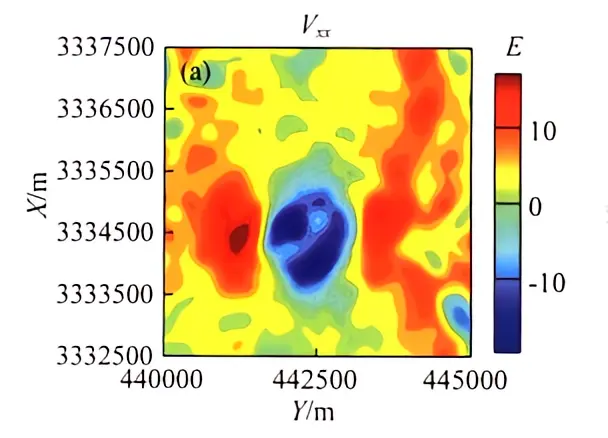文顿盐丘地区重力梯度

在计算机科学领域，全曲率可应用于无参考视频稳定质量评价算法中，从而改进对剧烈的抖动敏感或与主观评价结果一致性不高等问题。这种改进算法首先检测相邻两帧图像的特征点，计算相邻帧间单应变换；然后将单应变换映射到李群空间形成运动路径；最后借助离散测地逼近方法计算运动路径全曲率，以此衡量运动路径平滑程度，进而评价视频稳定程度。该算法获得的视频稳定评价结果与人眼主观评价结果的相关性达到97%，相比于帧间保真度、频域分析等现有评价算法提高20%以上。

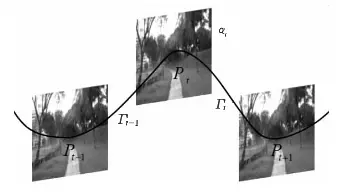单应变换路径的曲率表示