奇数(英文:odd integer)亦称单数,是一类重要的整数,其定义为:整数集Z中,不能被2整除的叫奇数,数学形式可表述为:2n±1(n为整数)。
定义
编辑整数集
中,不能被
整除的叫奇数。其数学形式表述为:
。例如,奇数
。
简史
编辑古代
整数概念最早可追溯到远古时期,人们为了计量物体的个数,自然用手指或其他事物,与被计量的物体进行逐一比较,从而产生了最初的整数。约公元前6世纪,古希腊数学家毕达哥拉斯(Pythagoras)建立的毕达哥拉斯学派认为自然界的一切都是由数组成的,并将数分为奇数和偶数,认为偶数是阴性的,奇数是阳性的,且奇数只能分成不相等的两部分。而后在形数的研究中,毕达哥拉斯学派注意到形与数的关系,如把连续的奇数相加,可得到正方形数;把连续的偶数相加,可得到长方形数等。后来,数学家柏拉图(Plato)把算术看成是关于奇数与偶数的科学,并在著作《巴门尼德》中记载了偶倍偶、奇倍奇、奇倍偶和偶倍奇等术语,改用现代化语言来表述即为偶数乘偶数、奇数乘奇数、奇数乘偶数和偶数乘奇数,体现了奇数与偶数之间的关系。约公元前300年,古希腊数学家欧几里得(Euclid)整理了前人的工作,写成13卷《几何原本》,其中关于奇数与偶数的相关内容记载在第九卷上。
柏拉图
近代
1826年,教育学家福禄贝尔(Friedrich Frobel)在著作《人类的教育》一书中指导教师用“1既不是偶数也不是奇数”的主张来教育学生。此外,福禄贝尔认为在两个相对地说不同的事物和概念之间存在着一个第三者,在两者中保持一定的平衡,把两者统一在自身之中。例如,在偶数和奇数之间有一个不属于两方之中任何一方的数。
 福禄贝尔
福禄贝尔
性质
编辑运算性质
加减法
(1)奇数
奇数
偶数;(2)奇数
偶数
奇数。
乘法
(1)奇数
偶数
偶数;(2)奇数
奇数
奇数;(3)奇数的任意非负整数(即正整数或零)次幂是奇数。
除法
在整数除法运算中,如果要让商是整数,这样的除法不是总能除尽的。由带余除法可知,整数
是奇数的充要条件是:
能表示为
的形式,其中
为整数。
特殊性质
(1)当
为奇数,且
时,
总能成立;(2)对任意的正整数
,总有:
- 任何一个整数
的完全平方数都可表示为从数
起的
个连续奇数的和;
- 任何一个正整数
的完全立方数,都可表示为首项为
和末项为
的
个连续奇数的和。
衍生概念
编辑奇数集
自然数的全体组成一个自然数集合,它可以分成奇数集和偶数集。其中,把奇数的全体组成一个集合
,称为奇数集。
相关概念
编辑偶数
定义:整数集
中,能被
整除的叫偶数,可用数学形式表述为:
。性质:(1)偶数
偶数
偶数;(2)偶数
偶数
偶数;(3)
是唯一的偶素数,其余的偶数都是合数;(4)任何一个非零正偶数
,总可以表示为
,其中
是正奇数,
是非零正整数。
是特殊的偶数,它不能表成
的形式;(5)任何偶数的平方总能被
整除;(6)任一偶数不与奇数相等。
相关猜想
编辑哥德巴赫猜想
猜想内容哥德巴赫猜想有两个,其中关于奇数的猜想是:每个不小于
的奇数都是三个奇素数之和。证明方法奇数哥德巴赫猜想最初在广义黎曼(Riemann)猜想成立的前提下,对于所有足够大的奇数成立。之后,苏联数学家维诺格拉多夫(VinogrADOv)用三角和方法证明了每一个大奇数都是三个奇素数之和,但没能定出下界。最终,在计算机验证的帮助下,奇数哥德巴赫猜想得以全部证明。猜想结论奇数哥德巴赫猜想已得到证明,但偶数哥德巴赫猜想仍然未得到解决。
类似理论
编辑函数的奇偶性
定义:设
为对称于原点的数集,
为定义在
上的函数,若对每一个
,都有
,则称
为
上的奇函数。若对每一个
,都有
,则称
为
上的偶函数。图像:如图,正弦函数
是一个奇函数,它的函数图形是关于原点
对称的。
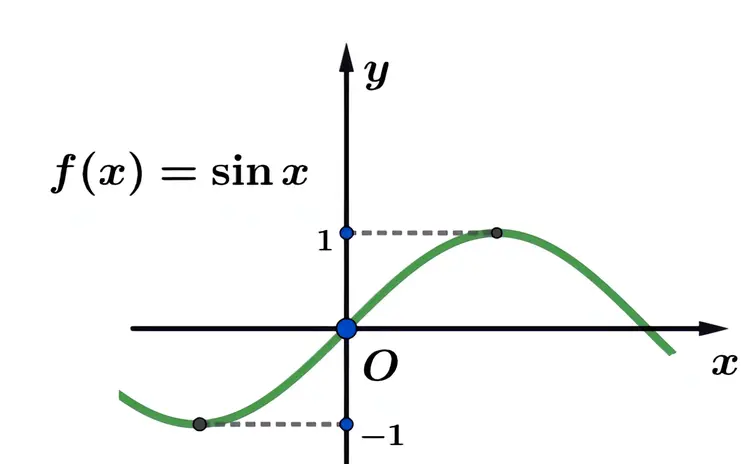 正弦函数
正弦函数
排列的奇偶性
定义:在一个
级排列
中,如果较大的元素
排在较小的元素
的左侧,则称
和
构成一个逆序。一个
级排列中逆序的总数,称为这个排列的逆序数,记为
或
逆序数为偶数的排列称为偶排列,逆序数为奇数的排列称为奇排列。例如:在
级排列中,因为
,所以排列
都是奇排列。
应用
编辑物理学
和
等偶数端口对称型光开关,它具有较强的扩容和重构能力,但在某些特定情况下,奇数端口非对称型光开关的也具有重要的应用。基于传统的成熟的信号光偏振控制技术,可设计一种
和
的非对称结构和奇数端口的交换开关,它具有结构简单紧凑、控制方便灵活、即插即用等特点。
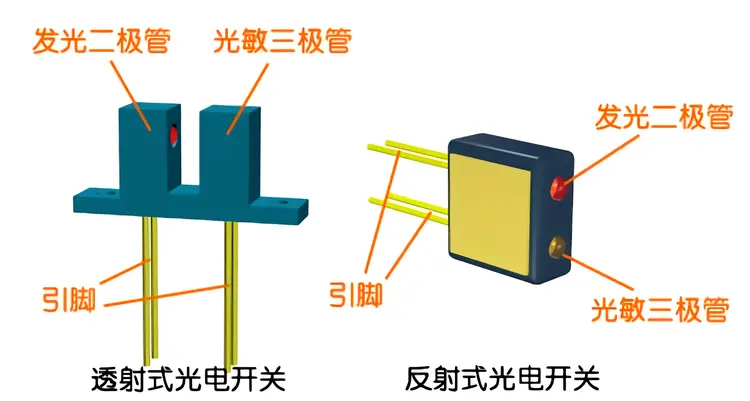
工程学
双作用叶片泵通过旋转定子可以改变排量成为变量泵,如果采用偶数叶片,可能会致使双作用变量叶片泵的瞬时流量的脉动量比较大,从而影响泵的性能。为了改善泵的瞬时流量性能,可采用奇数叶片的双变量叶片泵,它能有效地提高泵的瞬时流量性能。从瞬时流量性能的角度,变量双作用叶片泵可采用奇数叶片。

现实生活
美国州际高速公路的编号存在一定的规律,它的编号由一个或两个号码组成。通常,南北走向为奇数,如
等。由三个号码组成的高速公路,如果三个号码中的第一位数是单数,如
,说明该路为支路,进入城市后即终止。即从
号变成
号。

相关文化
编辑《世界奇妙物语 2000春之特别篇》是2000年在日本上映的一部电影,其中有一个关于“奇数”的篇章,主要讲述一个男人乘坐电车回家时,他发现所有人都坐在奇数的座位上,更奇怪的是,乘客们似乎是按照自己的座位顺序依次下车。
 电影海报
电影海报
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/1241769/
