粒子群优化

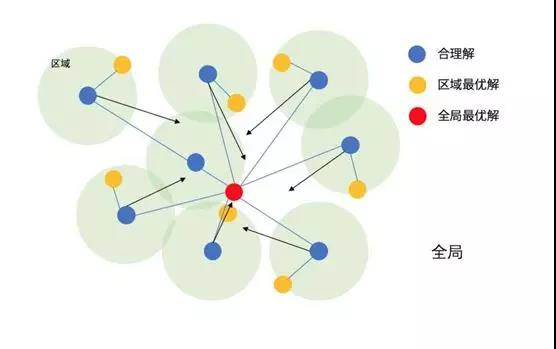
在计算科学中，粒子群优化(PSO)是一种计算方法，它通过迭代地尝试根据给定的质量度量改进候选解决方案来优化问题。它通过拥有一组候选解（这里称为粒子）来解决问题，并根据粒子位置和速度上的简单数学公式在搜索空间中移动这些粒子.每个粒子的运动受到其局部最佳已知位置的影响，但也会被引导到搜索空间中的最佳已知位置，这些位置随着其他粒子找到更好的位置而更新。预计这会将群体推向最佳解决方案。

粒子群优化最初归因于Kennedy、Eberhart和Shi，最初用于模拟社会行为，作为鸟群或鱼群中生物体运动的程式化表示。该算法被简化，并观察到它正在执行优化。Kennedy和Eberhart所著的这本书描述了PSO和群体智能的许多哲学方面。Poli对粒子群优化应用进行了广泛的调查。最近，Bonyadi和Michalewicz发表了关于粒子群优化的理论和实验工作的综合评论。

粒子群优化是一种元启发式算法，因为它对正在优化的问题几乎没有或根本没有假设，并且可以搜索非常大的候选解决方案空间。此外，粒子群优化不使用被优化问题的梯度，这意味着粒子群优化不需要像梯度下降法和拟牛顿法等经典优化方法所要求的优化问题是可微的。但是，诸如粒子群优化之类的元启发式算法并不能保证找到最佳解决方案。

粒子群优化参数的选择对优化性能有很大影响。因此，选择产生良好性能的粒子群优化参数已成为许多研究的主题。

粒子群优化参数也可以通过使用另一个重叠优化器来调整，这个概念被称为元优化，甚至在优化过程中进行微调，例如，通过模糊逻辑。

还针对各种优化场景调整了参数。

粒子群优化算法有效探索多个局部最小值的能力可以与基于梯度的局部搜索算法的能力相结合，以有效计算准确的局部最小值以产生基于梯度的PSO算法。在基于梯度的PSO算法中，PSO算法用于探索许多局部最小值并在深度局部最小值的吸引力盆地中定位一个点。然后使用高效的基于梯度的局部搜索算法来准确定位深层局部最小值。复杂高维成本函数的梯度和Hessian的计算通常计算成本高，并且在许多情况下无法手动进行，从而阻碍了基于梯度的PSO算法的广泛采用。然而，近年来，高质量符号自动微分(AD)软件的可用性导致对基于梯度的PSO算法的兴趣重新兴起。