什么是卡诺图
编辑卡诺图(KM或K-map)是一种简化布尔代数表达式的方法。卡诺(MauriceKarnaugh)于1953年提出,作为爱德华-维奇(EdwardW.Veitch)1952年提出的维奇图的改进,维奇图是对艾伦-马夸德(AllanMarquand)1881年逻辑图(又称马夸德图)的重新发现,但现在的重点是它对开关电路的效用。Veitch图也被称为Marquand-Veitch图,或者很少被称为Svoboda图,而Karnaugh图被称为Karnaugh-Veitch图(KV图)。卡诺图通过利用人类的模式识别能力,减少了对大量计算的需求。它还允许快速识别和消除潜在的竞赛条件。所需的布尔结果从真值表转移到一个二维网格上,在卡诺地图中,单元格以灰色代码排序,每个单元格的位置代表一个输入条件的组合。单元也被称为最小项,而每个单元的值代表布尔函数的相应输出值。最佳的1或0组被识别出来,它们代表了原始真值表中逻辑的典范形式的术语。这些项可以用来写一个最小的布尔表达式,代表所需的逻辑。卡诺图被用来简化现实世界的逻辑要求,以便可以用最少的逻辑门来实现它们。一个积和表达式(SOP)总是可以通过AND门进入OR门来实现,而一个积和表达式(POS)会导致OR门进入AND门。POS表达式给出了一个函数的补数(如果F是函数,那么它的补数将是F’)。卡诺图也可以用来简化软件设计中的逻辑表达。布尔条件,例如在条件语句中使用,会变得非常复杂,这使得代码难以阅读和维护。一旦最小化,典型的乘积之和和表达式就可以直接使用AND和OR逻辑运算符来实现。例子卡诺图是用来促进布尔代数函数的简化的。例如,考虑由以下真值表描述的布尔函数。下面是两个不同的符号,用布尔变量A、B、C、D和它们的倒数来描述同一函数的非简化布尔代数。
卡诺图的构造
编辑在上面的例子中,四个输入变量可以用16种不同的方式组合,所以真值表有16行,卡诺地图有16个位置。因此,卡诺地图被安排在一个4×4的网格中。行和列的索引(显示在卡诺图的顶部和左侧)是以格雷码而不是二进制数字顺序排列的。灰色代码确保每对相邻单元之间只有一个变量发生变化。完成的卡诺地图的每个单元都包含一个二进制数字,代表该输入组合的函数的输出。
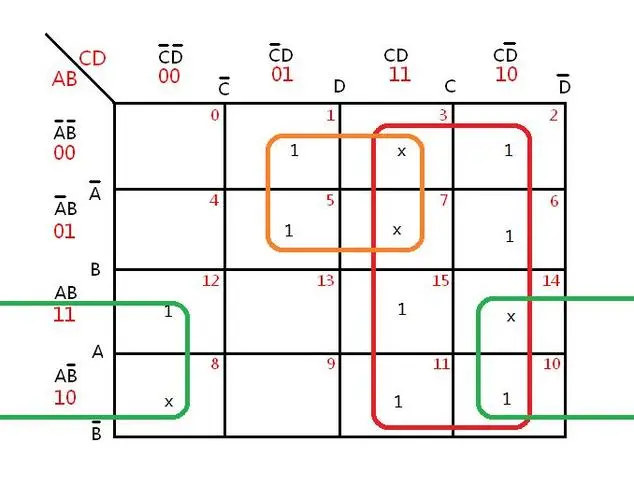
卡诺图的分组
编辑卡诺图构建完成后,它被用来为真值表中的信息找到一种最简单的形式–典型形式。Karnaugh图中相邻的1代表了简化表达式的机会。最终表达式的最小项(’minimalterms’)是通过包围地图中的1群来找到的。最小项组必须是矩形的,其面积必须是2的幂(即1、2、4、8…)。最小项的矩形应尽可能大而不包含任何0。组别可以重叠,以使每个组别变大。下面的例子中的最佳分组由绿线、红线和蓝线标记,红组和绿组是重叠的。红色组是一个2×2的正方形,绿色组是一个4×1的长方形,重叠的区域用棕色表示。单元通常用一个速记符号来表示,它描述了单元所覆盖的输入的逻辑值。例如,AD指的是覆盖A和D为真的2×2区域的单元,即上图中编号为13、9、15、11的单元。另一方面,AD指的是A为真、D为假(即D为真)的单元格。网格是环形连接的,这意味着矩形组可以绕过边缘(见图)。最右边的单元格实际上与最左边的单元格是”相邻”的,因为相应的输入值只相差一位。
内容由匿名用户提供,本内容不代表vibaike.com立场,内容投诉举报请联系vibaike.com客服。如若转载,请注明出处:https://vibaike.com/167756/
