PID控制器

比例-积分-衍生控制器（PID控制器或三期控制器）是一种采用反馈的控制回路机制，广泛用于工业控制系统和其他各种需要连续调制控制的应用。PID控制器连续计算误差值e ( t ) { {displaystyle e(t)}，作为期望设定点(SP)和测量过程变量(PV)之间的差值，并根据比例、积分和导数项（分别表示P、I和D）进行修正，因此得名。

在实际应用中，PID会自动对控制功能进行精确和反应灵敏的修正。一个日常的例子是汽车上的巡航控制，如果应用恒定的发动机功率，上坡时会降低速度。控制器的PID算法通过以受控方式增加发动机的功率输出，以最小的延迟和超调将测量的速度恢复到期望的速度。

PID的xxx个理论分析和实际应用是在船舶的自动转向系统领域，从20世纪20年代初开始发展。然后，它被用于制造业的自动过程控制，在那里，它首先被广泛地应用于气动控制器，然后是电子控制器。今天，PID概念被普遍用于需要精确和优化自动控制的应用中。

PID控制器的突出特点是能够利用比例、积分和导数这三个控制项对控制器输出的影响来进行精确和优化控制。右边的框图显示了这些项是如何产生和应用的原理。它显示了一个PID控制器，连续计算误差值e ( t ) {displaystyle e(t)}，作为期望设定点SP = r ( t ) {displaystyle {text{SP}}=r(t)}和测量过程变量PV = y ( t ) {displaystyle {text{PV}}=y(t)}之间的差异。e ( t ) = r ( t ) - y ( t ) {{displaystyle e(t)=r(t)-y(t)}，并应用基于比例、积分和导数项的校正。控制器试图通过调整控制变量u ( t ) {\displaystyle u(t)}，例如控制阀的开度，使其达到由控制项的加权和决定的新值，从而使误差在一段时间内最小。

项P与SP-PV误差e ( t ) {\displaystyle e(t)}的当前值成正比。例如，如果误差很大，通过使用增益因子Kp，控制输出将成比例地大。仅仅使用比例控制将导致设定点和过程值之间的误差，因为控制器需要一个误差来产生比例输出响应。在稳态过程条件下，会达到一个平衡，有一个稳定的SP-PV偏移。 期限I考虑了过去的SP-PV误差值，并将它们在一段时间内整合，产生I项。例如，如果在应用比例控制后有一个残余的SP-PV误差，积分项就会通过增加一个由于误差的历史累积值而产生的控制效应来消除残余的误差。当误差被消除后，积分项将停止增长。这将导致比例效应随着误差的减少而减少，但这被不断增长的积分效应所补偿。 D项是对SP-PV误差的未来趋势的最佳估计，基于其当前的变化率。它有时被称为预期控制，因为它实际上是通过施加由误差变化率产生的控制影响来寻求减少SP - PV误差的影响。变化越快，控制或阻尼效果越大。

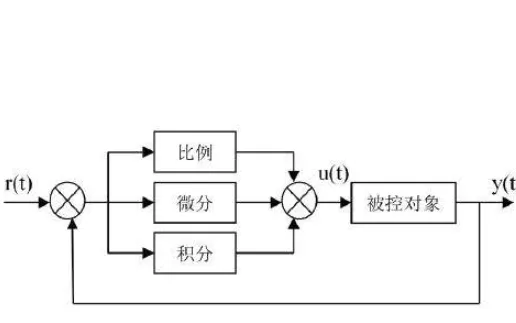
调谐 - 这些效果的平衡是通过回路调谐来实现的，以产生最佳控制功能。调谐常数在下面显示为K，必须为每个控制应用推导，因为它们取决于控制器外部完整环路的响应特性。这些取决于测量传感器的行为、最终控制元件（如控制阀）、任何控制信号的延迟和过程本身。常数的近似值通常可以在知道应用类型的情况下初步输入，但它们通常是通过在实践中引入设定点变化和观察系统反应来完善或调整过程。

控制作用--上面的数学模型和实际回路都对所有条款使用了直接控制作用，这意味着正误差的增加会导致控制输出修正的增加。如果有必要应用负的修正作用，则系统被称为反向作用。例如，如果流量回路中的阀门是100-0%的阀门开度，用于0-xxx的控制输出--意味着控制器的动作必须是反向的。