数据同化

数据同化是一门数学学科，旨在将理论（通常以数值模型的形式）与观察结果最佳地结合起来。 可能会寻求许多不同的目标——例如，确定系统的最佳状态估计，确定数值预测模型的初始条件，使用被观察系统的（例如物理）知识对稀疏观察数据进行插值， 根据观察数据训练模型来设置数值参数。 根据目标，可以使用不同的解决方法。 数据同化不同于其他形式的机器学习、图像分析和统计方法，因为它利用了被分析系统的动态模型。

数据同化最初发展于数值天气预报领域。 数值天气预报模型是描述大气动力学行为的方程式，通常编码为计算机程序。 为了使用这些模型进行预测，模型需要与当前大气状态非常相似的初始条件。 简单地将逐点测量插入数值模型并不能提供令人满意的解决方案。 由于仪器的质量和测量位置的已知准确度，现实世界的测量包含误差。 这些错误会导致模型不稳定，从而消除预测中任何水平的技能。 因此，需要更复杂的方法来使用所有可用数据初始化模型，同时确保保持数值模型的稳定性。 此类数据通常包括测量结果以及在进行测量的同时有效的先前预测。 如果反复应用，此过程开始将过去观察中的信息积累到所有后续预测中。

由于数据同化是从数值天气预报领域发展出来的，因此它最初在地球科学中受到欢迎。 事实上，在所有地球科学中被引用最多的出版物之一是应用数据同化来重建大气的观测历史。

传统上，数据同化已应用于使用简单的外推方法难以预测的混沌动力系统。 造成这种困难的原因是初始条件的微小变化会导致预测精度的巨大变化。 这有时被称为蝴蝶效应 - 对初始条件的敏感依赖性，在这种情况下，确定性非线性系统的一种状态的微小变化可能导致后来状态的巨大差异。

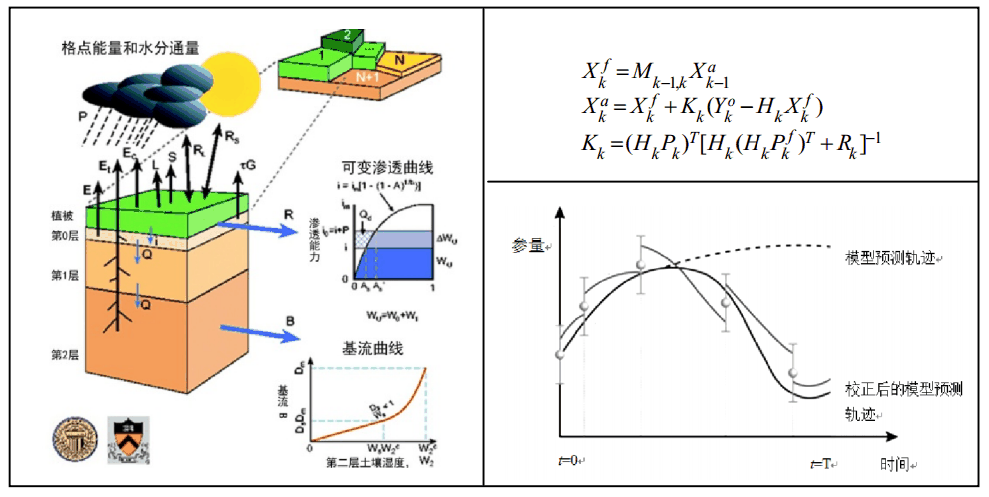
在任何更新时间，数据同化通常会进行预测（也称为xxx次猜测或背景信息），并根据一组观测数据和观测和预测中存在的估计误差对预测进行修正 本身。 预测与当时观测值之间的差异称为偏离或创新（因为它为数据同化过程提供了新信息）。 将加权因子应用于创新，以确定应根据观察到的新信息对预测进行多少修正。 基于对由加权因子乘以创新确定的预测的修正，对系统状态的最佳估计称为分析。 在一个维度上，计算分析可以像形成预测值和观察值的加权平均值一样简单。 在多个维度上，问题变得更加困难。 数据同化的大部分工作都集中在根据对系统错误的复杂了解来充分估计适当的加权因子。

测量通常来自真实世界的系统，而不是模型对该系统的不完整表示，因此称为观察算子的特殊函数（通常用 h() 表示非线性算子或 H 表示其非线性算子） 线性化）需要将建模变量映射到可以直接与观察值进行比较的形式。

一种常见的数学哲学观点是将数据同化视为贝叶斯估计问题。 从这个角度来看，分析步骤是贝叶斯定理的应用，整个同化过程是递归贝叶斯估计的一个例子。 然而，概率分析通常被简化为计算上可行的形式。 在一般情况下，可以通过 Fokker-Planck 方程及时推进概率分布，但这对于高维系统是不可行的； 因此，取而代之的是使用对概率分布的简化表示进行操作的各种近似值。