费米面

在凝聚态物理学中，费米面是倒易空间中的表面，它在零温度下将占据电子态与未占据电子态分开。 费米面的形状来源于晶格的周期性和对称性以及电子能带的占据。 费米面的存在是泡利不相容原理的直接结果，该原理允许每个量子态最多有一个电子。 对材料的费米面的研究被称为费米学。

考虑 N {dISPlaystyle N} 粒子的无自旋理想费米气体。 根据费米-狄拉克统计，能量为 ε i {diSPlaystyle epsilon _{i}} 的状态的平均占据数由下式给出

⟨ n i ⟩ = 1 e ( ϵ i − μ ) / k B T + 1 , {displaystyle langle n_{i}rangle ={frac {1}{e{(epsilon _{i }-mu )/k_{rm {B}}T}+1}},}

在哪里，

• ⟨ n i ⟩ {displaystyle leftlangle n_{i}rightrangle } 是第 i t h {displaystyle i{th}} 状态的平均占有数
• ε i {displaystyle epsilon _{i}} 是第 i t h {displaystyle i{th}} 态的动能
• μ {displaystyle mu } 是化学势（在零温度下，这是粒子可以拥有的最大动能，即费米能量 E F {displaystyle E_{rm {F}}} )
• T {displaystyle T} 是绝对温度
• k B {displaystyle k_{rm {B}}} 是玻尔兹曼常数

假设我们考虑极限 T → 0 {displaystyle Tto 0} 。 然后我们有，

⟨ n i ⟩ → { 1 ( ϵ i < μ ) 0 ( ϵ i > μ ) 。 {displaystyle leftlangle n_{i}rightrangle to {begin{cases}1&(epsilon _{i}<mu )\ 0&(epsilon _{i}>mu )end{cases}}.}

根据泡利不相容原理，任何两个费米子都不可能处于同一状态。 因此，在最低能量状态下，粒子充满了费米能量以下的所有能级 E F {displaystyle E_{rm {F}}} ，这相当于说 E F {displaystyle E_{ rm {F}}} 是能级，低于该能级恰好有 N {displaystyle N} 状态。

在动量空间中，这些粒子填满了一个半径为 k F {displaystyle k_{rm {F}}} 的球，球的表面称为费米面。

金属对电、磁或热梯度的线性响应由费米面的形状决定，因为电流是由于费米能量附近的状态占用变化引起的。 在倒易空间中，理想费米气体的费米面是一个半径为

k F = p F ℏ = 2 m E F ℏ {displaystyle k_{rm {F}}={frac {p_{rm {F}}}{hbar }}={ frac {sqrt {2mE_{rm {F}}}}{hbar }}} ,

由价电子浓度决定，其中 ℏ {displaystyle hbar } 是约化的普朗克常数。 根据带隙的大小，费米能级落在带隙中的材料是绝缘体还是半导体。 当材料的费米能级落在带隙内时，就没有费米面。

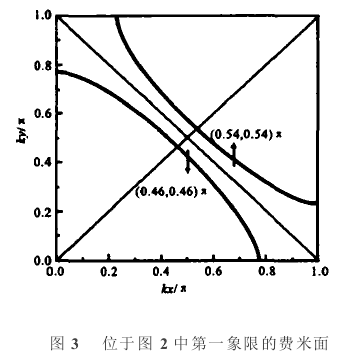
具有复杂晶体结构的材料可能具有相当复杂的费米面。 图 2 说明了石墨的各向异性费米面，由于多个带沿 k z {displaystyle mathbf {k} _{z}} 方向穿过费米能量，因此在其费米面中同时具有电子和空穴袋。 通常在金属中，费米面半径 k F {displaystyle k_{rm {F}}} 大于第一个布里渊区的大小，这导致费米面的一部分位于第二个（或 更高）区域。 与能带结构本身一样，费米面可以在扩展区域方案中显示，其中 k {displaystyle mathbf {k} } 允许具有任意大的值，或者在缩减区域方案中显示波矢量模 2 π a {textstyle {frac {2pi }{a}}} （在一维情况下）其中 a 是晶格常数。

在三维情况下，缩小区域方案意味着从任何波向量 k {displaystyle mathbf {k} } 中减去适当数量的倒易点阵向量 K {displaystyle mathbf {K} } 新的 k {displaystyle mathbf {k} } 现在比任何 K {displaystyle mathbf {k} } 更接近 k {displaystyle mathbf {k} } 空间中的原点 . 在费米能级具有高密度状态的固体在低温下变得不稳定，并倾向于形成基态，其中凝聚能来自于在费米面打开一个间隙。 这种基态的例子有超导体、铁磁体、Jahn-TELLEr 畸变和自旋密度波。

像电子这样的费米子的状态占用由费米-狄拉克统计数据控制，因此在有限温度下费米面相应地变宽。 原则上，所有费米子能级种群都受费米面约束，尽管该术语在凝聚态物理学之外通常不使用。

电子费米面是通过观察磁场 H {displaystyle H} 中传输特性的振荡来测量的。