阻尼

阻尼是振荡系统内部或之上的一种影响，具有减少或防止其振荡的作用。 在物理系统中，阻尼是由耗散振荡中存储的能量的过程产生的。 示例包括机械系统中的粘性阻力（液体的粘性会阻碍振荡系统，导致其减速；参见粘性阻尼）、电子振荡器中的阻力以及光学振荡器中的光吸收和散射。 不基于能量损失的阻尼在其他振荡系统中可能很重要，例如那些发生在生物系统和自行车中的振荡系统（例如悬架（力学））。 不要与摩擦力混淆，摩擦力是作用在系统上的耗散力。 摩擦会导致阻尼或成为阻尼的一个因素。

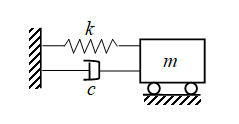
阻尼比是描述系统中的振荡在扰动后如何衰减的无量纲量度。 当许多系统从其静态平衡位置受到干扰时，它们会表现出振荡行为。 例如，悬挂在弹簧上的质量块，如果被拉动和释放，可能会上下弹跳。 在每次反弹时，系统往往会回到其平衡位置，但会超过平衡位置。 有时损失（例如摩擦）会使系统衰减，并可能导致振荡的振幅逐渐衰减至零或衰减。 阻尼比是描述振荡从一次反弹到下一次反弹衰减多快的量度。

阻尼比是一个系统参数，由 ζ (zeta) 表示，它可以从无阻尼 (ζ = 0)、欠阻尼 (ζ < 1) 到临界阻尼 (ζ = 1) 到过阻尼 (ζ > 1) 变化。

振荡系统的行为通常受到各种学科的关注，包括控制工程、化学工程、机械工程、结构工程和电气工程。 振荡的物理量变化很大，可能是高楼在风中的摇摆，也可能是电动机的速度，但归一化或无量纲化的方法可以方便地描述行为的共同方面。

根据存在的阻尼量，系统会表现出不同的振荡行为和速度。

• 在弹簧-质量系统完全无损的情况下，质量会无限期地振荡，每次反弹的高度都与最后一次相同。 这种假设情况称为无阻尼。
• 如果系统包含高损耗，例如，如果弹簧质量实验是在粘性流体中进行的，则质量可以缓慢地返回到其静止位置而不会过冲。 这种情况称为过阻尼。
• 通常，质量往往会超过其起始位置，然后返回，再次超过。 每次过冲都会耗散系统中的一些能量，并且振荡趋于零。 这种情况称为欠阻尼。
• 在过阻尼和欠阻尼情况之间，存在一定程度的阻尼，在该阻尼下系统将不会过冲并且不会产生单一振荡。 这种情况称为临界阻尼。 临界阻尼和过阻尼之间的主要区别在于，在临界阻尼下，系统会在最短时间内恢复平衡。

阻尼正弦波或阻尼正弦波是一种正弦函数，其幅度随着时间的增加趋近于零。 它对应于阻尼二阶系统的欠阻尼情况，或欠阻尼二阶微分方程。阻尼正弦波在科学和工程中很常见，只要谐波振荡器失去能量的速度快于提供能量的速度。真正的正弦波 starting at time = 0 从原点开始（振幅 = 0）。 由于与正弦波的相位差，余弦波从xxx值开始。 给定的正弦波形可能具有中间相位，具有正弦和余弦分量。 术语阻尼正弦波描述了所有此类阻尼波形，无论其初始相位如何。

通常假定的最常见的阻尼形式是线性系统中的形式。 这种形式是指数阻尼，其中连续峰值的外包络是指数衰减曲线。 也就是说，当您连接每条连续曲线的xxx值点时，结果类似于指数衰减函数。 指数阻尼正弦波的一般方程可以表示为： cos(omega t-phi )} 其中：

• y ( t ) {displaystyle y(t)} 为t时刻的瞬时振幅；
• A {displaystyle A} 是包络的初始振幅；
• λ {displaystyle lambda } 为衰减率，为自变量t时间单位的倒数；
• ϕ {displaystyle phi } 是 t = 0 时的相位角；
• ω {displaystyle omega } 是角频率。