广义力

广义力在拉格朗日力学中找到用途，它们在广义坐标中发挥共轭作用。 它们是从施加的力 Fi, i=1,..., n 中获得的，作用在一个系统上，该系统的配置根据广义坐标定义。 在虚功的表述中，每个广义力都是广义坐标的变化系数。

可以通过计算所施加力的虚功 δW 来获得广义力。

作用在粒子 Pi 上的力 Fi 的虚功 i=1,...,n 由下式给出

δ W = ∑ i = 1 n F i ⋅ δ r i

其中 δri 是粒子 Pi 的虚拟位移。

设每个粒子的位置向量 ri 是广义坐标 qj 的函数，j=1,...,m。 然后虚拟位移 δri 由下式给出

δ r i = ∑ j = 1 m ∂ r i ∂ q j δ q j , i = 1 , … , n ,

其中δqj是广义坐标qj的虚拟位移。

在虚功原理的应用中，从系统的速度中获得虚位移通常很方便。 对于n个粒子系统，令每个粒子Pi的速度为Vi，则虚位移δri也可以写成如下形式

δ r i = ∑ j = 1 m ∂ V i ∂ q ˙ j δ q j , i = 1 , … , n 。

达朗贝尔将粒子的动力学表述为所施加的力与惯性力（表观力）的平衡，称为达朗贝尔原理。 质量为 mi 的粒子 Pi 的惯性力为

F i ∗ = − m i A i , i = 1 , … , n ,

其中 Ai 是粒子的加速度。

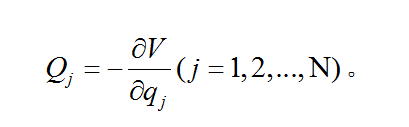
如果粒子系统的配置取决于广义坐标 qj，j=1,...,m，则广义惯性力由下式给出

Q j ∗ = ∑ i = 1 n F i ∗ ⋅ ∂ V i ∂ q ˙ j , j = 1 , … , m 。