谱密度

时间序列 x ( t ) {\displaystyle x(t)} 的功率谱 S x x ( f ) {\displaystyle S_{xx}(f)} 描述了功率在构成该信号的频率分量中的分布。 根据傅里叶分析，任何物理信号都可以分解成许多离散的频率，或者是连续范围内的频谱。 根据其频率内容分析的某个信号或某种信号（包括噪声）的统计平均值称为其频谱。

当信号的能量集中在一个有限的时间间隔内时，特别是如果它的总能量是有限的，人们可以计算能量谱密度。 更常用的是功率谱密度（或简称为功率谱），它适用于一直存在的信号，或者存在于足够长的时间段（特别是与测量持续时间相关）的信号，它也可以结束 无限的时间间隔。 功率谱密度 (PSD) 指的是每单位时间的谱能量分布，因为这种信号在所有时间的总能量通常是无限大的。 光谱分量的总和或积分产生总功率（对于物理过程）或方差（在统计过程中），与通过积分 x 2 ( t ) {\displaystyle x{2}(t) } 在时域上，如 Parseval 定理所规定的那样。

物理过程 x ( t ) {\displaystyle x(t)} 的谱通常包含有关 x {\displaystyle x} 性质的基本信息。 例如，乐器的音高和音色可以通过频谱分析立即确定。 光源的颜色由电磁波电场 E ( t ) {\displaystyle E(t)} 的频谱决定，因为它以极高的频率波动。 从诸如此类的时间序列中获取频谱涉及傅里叶变换和基于傅里叶分析的概括。 在许多情况下，时间域在实践中并没有具体使用，例如当色散棱镜用于在光谱仪中获得光谱时，或者当声音通过其对内耳听觉感受器的影响而被感知时，每个 其中对特定频率敏感。

然而，本文主要关注时间序列已知（至少在统计意义上）或直接测量（例如通过计算机采样的麦克风）的情况。 功率谱在统计信号处理和随机过程的统计研究以及物理学和工程学的许多其他分支中都很重要。 通常，该过程是时间的函数，但可以类似地讨论根据空间频率分解的空间域中的数据。

任何可以表示为随时间变化的变量的信号都有相应的频谱。 这包括熟悉的实体，例如可见光（被感知为颜色）、音符（被感知为音高）、无线电/电视（由它们的频率或有时由波长指定）甚至地球的规律自转。 当以频谱的形式查看这些信号时，会揭示接收到的信号或产生这些信号的潜在过程的某些方面。 在一些情况下，频谱可以包括对应于正弦波分量的明显峰值。 此外，可能存在与基波峰值的谐波相对应的峰值，表明周期信号不是简单的正弦曲线。 或者，连续频谱可能显示狭窄的频率间隔，这些频率间隔与共振相对应而得到强烈增强，或者频率间隔包含几乎为零的功率，如陷波滤波器所产生的那样。

在物理学中，信号可能是一种波，例如电磁波、声波或机械振动。 信号的功率谱密度 (PSD) 将信号中存在的功率描述为每单位频率的频率函数。 功率谱密度通常以瓦特/赫兹 (W/Hz) 表示。

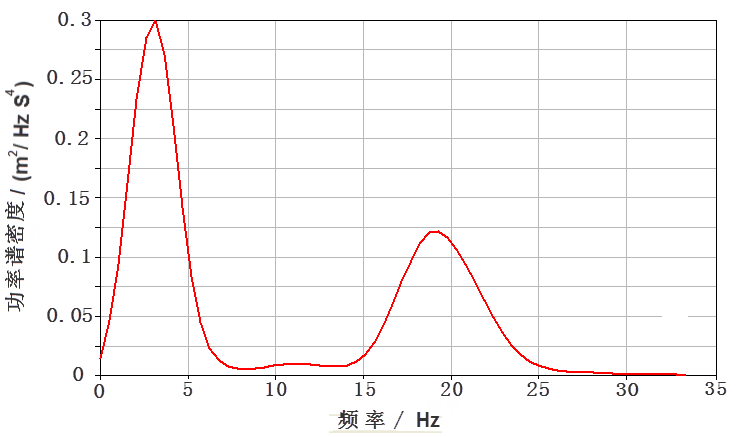
例如，当信号仅根据电压定义时，没有与规定幅度相关联的xxx功率。 在这种情况下，功率简单地根据信号的平方来计算，因为这总是与该信号传递到给定阻抗的实际功率成正比。 因此，对于 PSD，可以使用 V2 Hz−1 的单位。 能量谱密度 (ESD) 的单位为 V2 s Hz−1，因为能量的单位是功率乘以时间（例如，瓦时）。

在一般情况下，PSD 的单位将是每单位频率的方差单位的比率； 因此，例如，随时间（以秒为单位）的一系列位移值（以米为单位）的 PSD 单位为米平方每赫兹，m2/Hz。在随机振动分析中，g2 Hz−1 的单位经常是 用于加速度的PSD。