相速度

对于表面重力波，在大多数情况下，水粒子速度远小于相速度。

波的相速度是波在任何介质中传播的速率。 这是波的任何一个频率分量的相位传播的速度。 对于这样的分量，波的任何给定相位似乎都以相速度传播。 相速度根据波长 λ (lambda) 和时间周期 T 给出：

v p = λ T ,等价地，根据波的角频率 ω 和波数（或角波数）k，它表示每单位时间的角度变化，

v p = ω k 。

为了获得这个方程的一些基本直觉，我们考虑传播（余弦）波 A cos(kx − ωt)。 我们想看看波的特定相位传播的速度有多快。 例如，我们可以选择 kx - ωt = 0，即xxx个波峰的相位。 这意味着 kx = ωt，因此 v = x / t = ω / k。

形式上，我们让相位 φ = kx - ωt 并立即看到 ω = -dφ / dt 和 k = dφ / dx。 所以，紧随其后的是

∂ x ∂ t = − ∂ ϕ ∂ t ∂ x ∂ ϕ = ω k 。结果，我们观察到角频率和波矢之间的反比关系。 如果波具有更高频率的振荡，则必须缩短波长以使相速度保持恒定。 此外，在某些情况下（例如反常色散），电磁辐射的相速度可能会超过真空中的光速，但这并不表示任何超光速信息或能量转移。 阿诺德索末菲和莱昂布里渊等物理学家在理论上对其进行了描述。

一组波的群速度定义为

v g = ∂ ω ∂ k 。

当多个正弦波一起传播时，波的合成叠加会产生包络波以及位于包络内的载波。 这通常出现在无线通信中，采用调制、幅度和/或相位的变化来发送数据。 为了获得对该定义的一些直觉，我们考虑（余弦）波 f(x, t) 与其各自的角频率和波矢量的叠加。

因此，我们有两个波的乘积：由 f1 形成的包络波和由 f2 形成的载波。 我们称包络波的速度为群速度。 我们看到 f1 的相速度是

ω 2 − ω 1 k 2 − k 1 。

在连续微分情况下，这成为群速度的定义。

在电磁学和光学的背景下，频率是波数的某个函数 ω(k)，因此一般来说，相速度和群速度取决于特定的介质和频率。 光速 c 与相速度 vp 的比值称为折射率，n = c / vp = ck / ω。

这样，我们就可以得到电磁学群速度的另一种形式。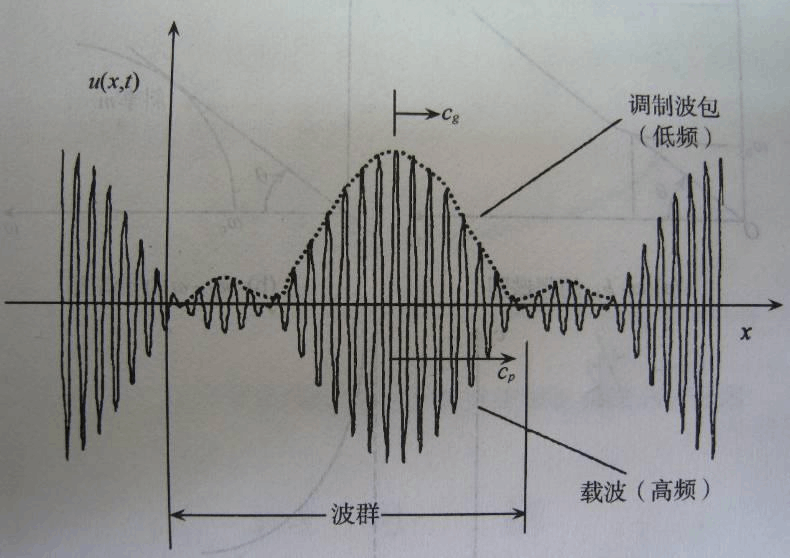

然后我们可以重新排列上面的内容以获得

v g = ∂ w ∂ k = c n + ω ∂ n ∂ ω 。

从这个公式中，我们看到只有当折射率为常数 dn / dk = 0 时，群速度才等于相速度。出现这种情况时，介质称为非色散，与色散相反，其中各种性质 介质的大小取决于频率 ω。 关系 ω = ω(k) 被称为介质的色散关系。