正弦曲线

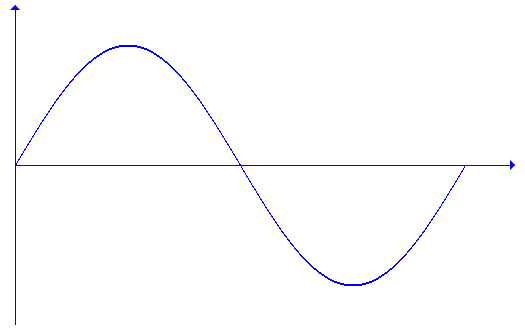
正弦波、正弦波或正弦波是根据正弦三角函数定义的数学曲线，它是图形。 它是一种连续波，也是一种光滑的周期函数。 它经常出现在数学以及物理、工程、信号处理和许多其他领域。

它作为时间 (t) 函数的最基本形式是： y ( t ) = A sin ⁡ ( 2 π f t + φ ) = A sin ⁡ ( ω t + φ ) 其中：

• A，振幅，函数与零的峰值偏差。
• f，普通频率，每秒发生的振荡（周期）数。
• ω = 2πf，角频率，函数自变量的变化率，单位为弧度每秒。
• φ，相位，指定（以弧度为单位）在其周期中 t = 0 时的振荡位置。当 φ非零时，整个波形 似乎在时间上偏移了 φ/ω 秒。 负值代表延迟，正值代表提前。

正弦曲线 5 秒的 220 赫兹正弦波。 这是由 f = 每秒振荡 220 次的正弦函数描述的声波。

正弦波在物理学中很重要，因为当它添加到另一个具有相同频率和任意相位和幅度的正弦波时，它会保持其波形。 它是xxx具有此属性的周期波形。 此属性导致它在傅立叶分析中的重要性，并使其在声学上xxx。

一般来说，函数还可能有：

• 一个空间变量x表示波在维度上传播的位置，一个特征参数k称为波数（或角波数），表示角频率ω与线速度（速度）之间的比例关系 传播) ν;
• 非零中心幅度，D

这个等式给出了一个单一维度的正弦波； 因此，上面给出的广义方程给出了波在时间 t 处的位置 x 沿单条线的位移。例如，这可以被认为是波沿导线的值。

在两个或三个空间维度中，如果位置 x 和波数 k 被解释为向量，并且它们的积被解释为点积，则相同的方程描述了一个行进的平面波。 对于更复杂的波浪，例如将石头扔进池塘后水波的高度，需要更复杂的方程式。

术语正弦曲线描述具有正弦波特征的任何波。 因此，余弦波也被称为正弦波，因为 cos ⁡ ( x ) = sin ⁡ ( x + π / 2 ) ，它也是具有 π/2 弧度相移的正弦波。 由于这个先机，人们常说余弦函数超前于正弦函数或正弦滞后于余弦。 因此，术语正弦波统指具有任何相位偏移的正弦波和余弦波。

这种波型在自然界中经常出现，包括风波、声波和光波。

人耳可以将单个正弦波识别为听起来清晰，因为正弦波表示没有谐波的单一频率。

对于人耳来说，由多个正弦波组成的声音会有可察觉的谐波； 添加不同的正弦波会产生不同的波形，从而改变声音的音色。

除了基波之外，高次谐波的存在会导致音色的变化，这就是为什么相同的音符（相同的频率）在不同的乐器上演奏时听起来不同的原因。 另一方面，如果声音包含非周期波和正弦波（周期性的），则声音会被感知为嘈杂，因为噪声的特征是非周期性或具有非重复模式。