学习率

在机器学习和统计学中，学习率是优化算法中的一个调整参数，它决定了每次迭代的步骤大小，同时向损失函数的最小值移动。

由于它影响到新获得的信息在多大程度上覆盖了旧信息，它比喻为机器学习模型的学习速度。

在自适应控制文献中，学习率通常被称为增益。

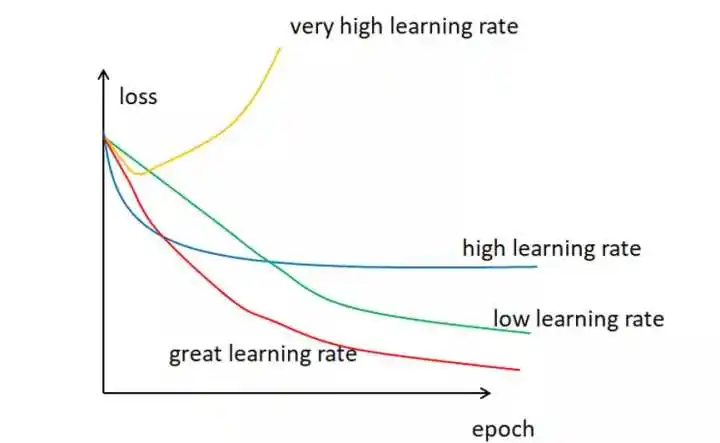
在设置学习率时，需要在收敛率和过冲之间进行权衡。虽然下降方向通常由损失函数的梯度决定，但学习率决定了在这个方向上迈出多大的一步。

过高的学习率会使学习跳过最小值，但过低的学习率要么需要太长的时间来收敛，要么卡在一个不理想的局部最小值。为了实现更快的收敛，防止振荡和陷入不理想的局部最小值，学习率在训练过程中通常是根据学习率计划或通过使用自适应学习率来改变的。

学习率及其调整也可以因参数而异，在这种情况下，它是一个对角矩阵，可以解释为牛顿方法中Hessian矩阵的近似值。

学习率与准牛顿方法和相关优化算法中的非精确线搜索确定的步长有关。在进行直线搜索时，小批量子采样（MBSS）会影响损失函数的特性，学习率需要沿着这个函数来解决。

静态MBSS保持沿搜索方向的小批量固定，导致沿搜索方向的损失函数平滑。

动态MBSS在每次函数评估时都会更新小批，导致沿搜索方向的损失函数是点状不连续的。

适应性地解决静态MBSS损失函数的学习率的线路搜索包括抛物线近似线路（PAL）搜索。

适应性地解决动态MBSS损失函数的学习率的线路搜索包括概率线路搜索、仅梯度线路搜索（GOLS）和二次逼近。

初始率可以保留为系统默认值，也可以使用一系列技术来选择。

学习率计划在学习过程中改变学习率，最常见的是在epochs/iterations之间改变。

这主要是通过两个参数完成的：衰减和动量。

有许多不同的学习率计划，但最常见的是基于时间、基于步骤和指数的。

衰减的作用是将学习稳定在一个好的位置，避免振荡，这种情况可能出现在过高的恒定学习率使学习在一个最小值上来回跳动，它由一个超参数控制。

动量类似于一个从山上滚下来的球；我们希望球能在山上的最低点（对应于最低的误差）安家。

当误差成本梯度长期朝向同一方向时，动量既能加快学习速度（增加学习率），也能通过"滚过"小颠簸来避免局部最小值。

动量是由一个类似于球的质量的超参数控制的，必须手动选择--太高了，球会滚过我们希望找到的最小值，太低了，它将无法实现其目的。

考虑动量的公式比衰减的公式更复杂，但最常见的是内置于深度学习库中，如Keras。基于时间的学习计划会根据前一个时间迭代的学习率来改变学习率。

考虑到衰减的因素，学习率的数学公式是。基于步骤的学习时间表根据一些预先定义的步骤改变学习率。

衰减应用公式在此定义为。{displaystyler}是每次下降时学习率应该变化的程度（0.5相当于减半），r对应于下降率，或者说下降率的频率（10对应于每10次迭代的下降）。

下限函数({displaystylelfloordotsrfloor})在这里，对于所有小于1的值，它的输入值都会下降到0。指数学习计划与基于步骤的学习计划类似，但我们使用的不是步骤，而是递减的指数函数。