双电层力

双电层力发生在液体（通常是水）中的带电物体之间。 该力作用的距离与德拜长度相当，大约为一到十分之几纳米。 这些力的强度随着表面电荷密度（或表面电势）的大小而增加。

对于两个带类似电荷的物体，这种力是排斥力，并且在距离较远时呈指数衰减。对于带电不等的物体以及最终距离较近的物体，这些力也可能具有吸引力。

将这种双层力与范德华力结合在一起，以估计胶体粒子之间的实际相互作用潜力。

双电层在水溶液中的带电表面（或其他带电物体）附近形成。 在这个双层中，xxx层对应于带电表面。 这些电荷可能源自紧密吸附的离子、离解的表面基团或晶格内的取代离子。

第二层对应于扩散层，其中包含由累积的抗衡离子和耗尽的离子组成的中和电荷。这两个物体之间产生的电位分布导致这些物体之间的间隙内的离子浓度相对于本体溶液存在差异。

这些差异会产生渗透压，从而在这些物体之间产生一种力。

当用肥皂洗手时，很容易感受到这些力。

吸附肥皂分子使皮肤带负电，滑溜感是由强烈排斥的双层力造成的。

这些力在许多胶体或生物系统中进一步相关，并且可能是它们的稳定性、胶体晶体的形成或它们的流变特性的原因。

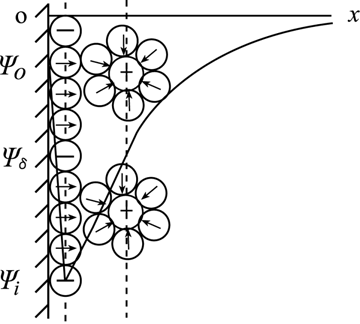
描述双电层最流行的模型是泊松-玻尔兹曼 (PB) 模型。该模型同样可以用于评估双层力。 让我们在平面几何的情况下讨论这个模型，如右图所示。 在这种情况下，带电界面附近的电势分布 ψ(z) 将仅取决于位置 z。 相应的泊松方程以 SI 单位读取

d 2 ψ d z 2 = − ρ ϵ 0 ϵ {\displaystyle {\frac {d{2}\psi }{dz{2}}}=-{\frac {\rho }{\epsilon _{0}\epsilon }}}

其中 ρ 是每单位体积的电荷密度，ε0 是真空的介电常数，ε 是液体的介电常数。 对于由带电荷±q的阳离子和阴离子组成的对称电解质，电荷密度可表示为

ρ = q ( c + − c − ) {\displaystyle \rho =q(c_{+}-c_{-})}

其中 c± = N±/V 是阳离子和阴离子的浓度，其中 N± 是它们的数量，V 是样品体积。 考虑到离子的化学势是恒定的这一事实，这些曲线可以与电势相关联。 对于这两种离子，这种关系可以写成

μ ± = μ + ( 0 ) + k T ln ⁡ c ± ± q ψ {\displaystyle \mu _{\pm }=\mu _{+}{(0)}+kT\ln c_ {\pm }\pm q\psi }

其中 μ ± ( 0 ) {\displaystyle \mu _{\pm }{(0)}} 是参考化学势，T 是xxx温度，k 是玻尔兹曼常数。 可以通过在远离表面的地方应用相同的方程式来消除参考化学势，其中假定电位消失并且浓度达到体积浓度 cB。 浓度分布因此变为

c ± = c B e ∓ β q ψ {\displaystyle c_{\pm }=c_{\rm {B}}e{\mp \beta q\psi }}

其中 β = 1/(kT)。 该关系反映了能量为±qψ 的离子的玻尔兹曼分布。 将这些关系代入泊松方程得到 PB 方程

d 2 ψ d z 2 = q c B ϵ 0 ϵ [ e + β q ψ − e − β q ψ ] {\displaystyle {\frac {d{2}\psi }{dz{2}}}={ \frac {qc_{\rm {B}}}{\epsilon _{0}\epsilon }}[e{+\beta q\psi }-e{-\beta q\psi }]}

两块板之间的电势分布通常通过对该方程进行数值求解来获得。

一旦知道了潜在的分布，板之间每单位面积的力表示为分离压力 Π 可以如下获得。 起点是恒温下双组分系统的 Gibbs–Duhem 关系

− V d Π + N + d μ + + N − d μ − = 0 {\displaystyle -Vd\Pi +N_{+}d\mu _{+}+N_{-}d\mu _ {-}=0}

引入浓度 c± 并使用上面给出的化学势 μ± 的表达式发现

d Π = k T ( d c + + d c − ) + q ( c + − c − ) d ψ {\displaystyle d\Pi =kT(dc_{+}+dc_{-})+q(c_{+ }-c_{-})d\psi }

浓度差可以用泊松方程消除，得到的方程可以从板的无限分离到实际分离 h 积分。