简谐运动

在力学和物理学中，简谐运动（有时缩写为 SHM）是一种特殊类型的物体周期性运动，由惯性力（与物体远离静态平衡位置的加速度成正比）和恢复力之间的动态平衡引起 运动物体上的力与物体位移的大小成正比，作用于物体的平衡位置。 如果不受摩擦或任何其他能量耗散的抑制，它会导致振荡，由无限期持续的正弦曲线描述。

简谐运动可以作为各种运动的数学模型，但以弹簧上的质量块在胡克定律给出的线性弹性恢复力作用下的振荡为代表。 运动在时间上呈正弦曲线，并表现出单一的共振频率。 其他现象可以通过简谐运动来建模，包括单摆的运动，尽管要成为一个精确的模型，摆末端物体上的净力必须与位移成正比（即使如此， 当摆动的角度很小时，它只是一个很好的近似；参见小角度近似）。 简谐运动也可用于模拟分子振动。

简谐运动为通过傅立叶分析技术表征更复杂的周期运动提供了基础。

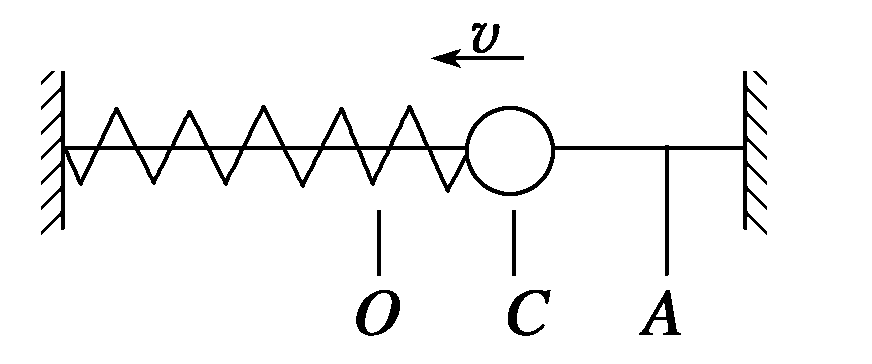
质点沿直线运动，加速度的方向总是指向直线上的一个定点，其大小与到该定点的距离成正比，这种运动称为简谐运动。

在图中，显示了一个简谐振子，它由连接在弹簧一端的重物组成。 弹簧的另一端连接到刚性支撑物，例如墙壁。 如果系统在平衡位置保持静止，则没有净力作用在质量上。 但是，如果质量块偏离平衡位置，弹簧就会产生一个符合胡克定律的恢复弹力。

对于任何简单的机械谐振子：

• 当系统偏离平衡位置时，遵循胡克定律的恢复力会使系统恢复平衡。

一旦质量从其平衡位置移动，它就会受到净恢复力。 结果，它加速并开始回到平衡位置。 当质量移近平衡位置时，恢复力减小。 在平衡位置，净恢复力消失。 然而，在 x = 0 时，由于恢复力赋予的加速度，质量具有动量。 因此，质量继续超过平衡位置，压缩弹簧。 然后净恢复力使其减速直到其速度达到零，随后它再次加速回到平衡位置。

只要系统没有能量损失，质量就会继续振荡。 因此简谐运动是一种周期运动。 如果能量在系统中丢失，则质量会出现阻尼振荡。

请注意，如果实空间和相空间图不共线，则相空间运动变为椭圆形。 封闭的面积取决于振幅和xxx动量。

在牛顿力学中，对于一维简谐运动，运动方程是一个常系数的二阶线性常微分方程，可以利用牛顿第二定律和胡克定律得到 弹簧上的质量。