刚体

在物理学中，刚体（也称为刚体）是变形为零或小到可以忽略的固体。 无论施加在其上的外力或力矩如何，刚体上任意两个给定点之间的距离在时间上保持不变。 刚体通常被认为是质量的连续分布。

在狭义相对论的研究中，完全刚体是不存在的； 并且只有当物体不以接近光速的速度运动时，才能假定它们是刚性的。 在量子力学中，刚体通常被认为是质点的集合。 例如，分子（由点质量组成：电子和原子核）通常被视为刚体（参见分子分类为刚性转子）。

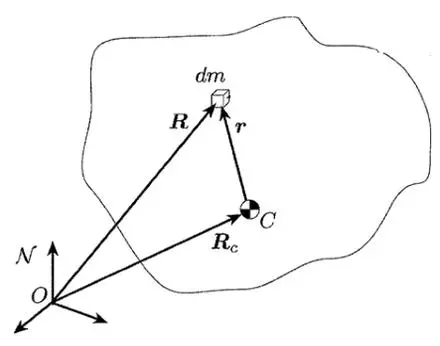
刚体的位置是组成它的所有粒子的位置。 为了简化这个位置的描述，我们利用物体是刚性的特性，即它的所有粒子彼此保持相同的距离。 如果物体是刚性的，则描述至少三个非共线粒子的位置就足够了。 这使得重建所有其他粒子的位置成为可能，前提是它们相对于三个选定粒子的时间不变位置是已知的。 然而，通常使用不同的、数学上更方便但等效的方法。 整个身体的位置表示为：

• 身体的线性位置或位置，即身体的一个粒子的位置，特别选择作为参考点（通常与身体的质心或质心重合），以及</li >
• 身体的角度位置（也称为方向或姿态）。

因此，刚体的位置有两个分量：分别是线性分量和角度分量。 描述刚体运动的其他运动学和动力学量也是如此，例如线速度和角速度、加速度、动量、冲量和动能。

线性位置可以用一个矢量表示，其尾部位于空间中的任意参考点（所选坐标系的原点），其尖端位于刚体上任意感兴趣的点，通常与其质心重合或 质心。 该参考点可以定义固定到身体的坐标系的原点。

有几种方法可以用数字来描述刚体的方向，包括一组三个欧拉角、四元数或方向余弦矩阵（也称为旋转矩阵）。 所有这些方法实际上都定义了一个基组（或坐标系）的方向，该基组（或坐标系）相对于身体（即与身体一起旋转）具有固定方向，相对于另一个基组（或坐标系）的运动 观察刚体。 例如，相对于飞机具有固定方向的基集可以定义为一组三个正交单位向量 b1、b2、b3，使得 b1 平行于机翼的弦线并指向前方，b2 垂直于 对称平面并向右，b3 由叉积 b 3 = b 1 × b 2 {\displaystyle b_{3}=b_{1}\times b_{2}} 给出。

一般来说，当一个刚体运动时，它的位置和方向都会随时间变化。 在运动学意义上，这些变化分别称为平移和旋转。 事实上，刚体的位置可以看作是身体从假设参考位置开始的假设平移和旋转（旋转平移）（不一定与身体在其运动过程中实际采取的位置一致）。

速度（也称为线速度）和角速度是相对于参考系测量的。

刚体的线速度是一个矢量，等于其直线位置的时间变化率。 因此，它是固定在身体上的参考点的速度。 在纯平移运动（没有旋转的运动）中，刚体上的所有点都以相同的速度运动。 但是，当运动涉及旋转时，身体上任意两点的瞬时速度一般不会相同。 旋转体的两点只有恰好位于与瞬时旋转轴平行的轴上时才会具有相同的瞬时速度。

角速度是描述刚体方位变化的角速度及其旋转的瞬时轴（这个瞬时轴的存在由欧拉旋转定理保证）的矢量。 刚体上的所有点始终经历相同的角速度。 在纯旋转运动中，身体上的所有点都会改变位置，除了那些位于 i 上的点。