柯西应力张量

在连续介质力学中，柯西应力张量 σ {\displaystyle {\boldsymbol {\sigma }}} ，真应力张量，或简称为应力张量，是以 Augustin-Louis Cauchy 命名的二阶张量。 张量由九个分量 σ i j {\displaystyle \sigma _{ij}} 组成，它们完全定义了处于变形状态、位置或配置的材料内部某一点的应力状态。 张量将单位长度方向矢量 e 与穿过垂直于 e 的假想表面的牵引矢量 T(e) 相关联

应力张量和牵引力矢量的国际单位均为 N/m2，对应于应力标量。 单位向量是无量纲的。

柯西应力张量服从坐标系变化下的张量变换规律。 这种转换定律的图形表示是应力的莫尔圆。

柯西应力张量用于对经历小变形的物质体进行应力分析：它是线性弹性理论的核心概念。 对于大变形，也称为有限变形，需要其他应力测量，例如 Piola–Kirchhoff 应力张量、Biot 应力张量和 Kirchhoff 应力张量。

根据线性动量守恒原理，如果连续体处于静平衡状态，则可以证明连续体各质点的柯西应力张量分量均满足平衡方程（Cauchy's equations of 零加速度运动）。 同时，根据角动量守恒原理，平衡要求任意一点的力矩之和为零，从而得出应力张量对称的结论，因此只有六个独立的应力分量 ，而不是原来的九个。 然而，在偶应力存在的情况下，即每单位体积的力矩，应力张量是非对称的。 当克努森数接近一时也是如此，K n → 1 {\displaystyle K_{n}\rightarrow 1} ，或者连续体是非牛顿流体，这会导致旋转不不变 流体，例如聚合物。

有一些与应力张量相关的不变量，其值不依赖于所选的坐标系或应力张量所作用的面积元素。 这些是应力张量的三个特征值，称为主应力。

欧拉-柯西应力原理指出，在任何分隔身体的表面（实数或虚数）上，身体的一部分对另一部分的作用等价于（等量）分布力的系统，并在分隔表面上耦合 体

为了制定欧拉-柯西应力原理，考虑一个假想表面 S {\displaystyle S} 通过内部材料点 P {\displaystyle P} 将连续体分成两段，

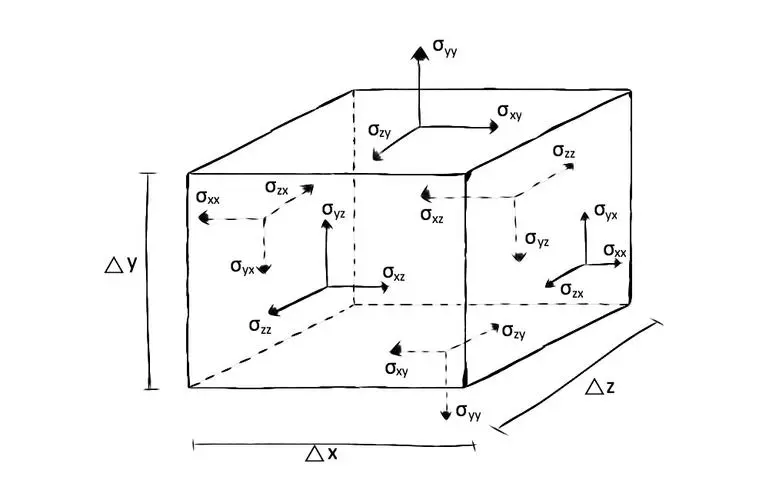
遵循牛顿和欧拉的经典动力学，物质体的运动是由外部施加的力的作用产生的，这些力被假定为两种：

当身体受到外表面力或接触力 F {\displaystyle \mathbf {F} } 时，遵循欧拉运动方程，内部接触力和力矩在身体中从一个点传递到另一个点，并且 通过划分从一个部分到另一个部分。