角动量

角动量（angular momentum），又称动量矩，描述物体转动状态的物理量。

自从开普勒提出了他的第二行星运动定律，人们就已获知，在相同的时间间隔内，太阳和行星之间的连线扫过的面积是相等的。牛顿提出了独特的几何证明，进一步证实了太阳引力的吸引力是导致所有开普勒定律的原因。在《原理》一书中，牛顿在讨论xxx运动定律的例子时，暗示了角动量的概念。他通过对面积定律的几何证明，间接证明了在受到中心力的情况下，角动量是守恒的。莱昂哈德·欧拉（Leonhard Euler）、丹尼尔·伯努利（Daniel Bernoulli）和帕特里克·达西都（Patrick Darcy）都从面速度守恒的角度理解角动量。1736 年，欧拉像牛顿一样，在《力学》一书中提到了一些角动量方程，但并未对这些方程进行进一步的探讨。 伯努利在1744 年的一封信中写到了“旋转运动的力矩”，这可能是我们现在理解的xxx个角动量概念。1799 年，皮埃尔-西蒙·拉普拉斯 (Pierre-Simon Laplace)首次意识到固定平面与旋转相关——拉普拉斯不变平面。路易·波因索（Louis Poinsot）于1803年开始将旋转表示为垂直于旋转的线段，并详细阐述了“力矩守恒”。威廉·兰金（William Rankine）在1858 年的《应用力学手册》首次定义了现代意义上的角动量：一条线，其长度与角动量的大小成正比，其方向垂直于物体和固定点的运动平面。当从线的末端观察物体的运动时，物体的半径矢量符合右螺旋法则。

角动量是一个矢量（更准确地说，是伪矢量），表示物体绕特定轴的旋转惯量和旋转速度（以弧度/秒为单位）的乘积。然而，如果粒子的轨迹位于单个平面内，则可以忽略角动量的矢量性质，并将其视为标量（更准确地说，伪标量）。角动量可以被认为是线性动量在旋转过程中的表现。因此，正如线性动量

与质量

和线速度

成正比，

，角动量

与转动惯量

和以弧度/秒为单位的角速度

成正比，

。与仅取决于物体数量的质量不同，转动惯量还取决于旋转轴的位置和物体密度的分布。与不依赖于原点选择的线速度不同，轨道角速度的测量始终是相对于一个固定的原点进行的。因此，严格来说，

应该是指相对于该中心的角动量。对于单个粒子的圆周运动，我们可以使用

和

将角动量化简为：

。如果使用垂直于半径向量的运动分量，这一简单的分析也适用于非圆周运动：

,其中

是运动的垂直分量。重新排列，代入到原式，得到：

，其中

是力臂的长度，是从原点垂直落到粒子路径上的一条线。术语动量矩定义为力臂长度与线性动量的叉积。

00:52

三分钟了解角动量（来源：中科院物理所)

若物体运动时有一点固定不动，则相对于该点的总角动量L为：

，其中

、

、

分别是质点i的质量、相对该点的距离矢量以及速度。由于

是一个相对于物体的固定矢量，所以，相对于空间坐标系的速度

完全由刚体绕固定点的转动所引起。因此上式可以写成：

，把三重矢积展开，即有：

，再次展开，角动量的x分量为：

。角动量的每一个分量都是角速度的所有分量的线性函数，角动量矢量通过线性变换与角速度矢量相关联。为了强调其与线性变换式的相似性，我们可以将角动量的x分量写成：

，

等九个系数是变换矩阵的九个元素，其中对角元就是通常所说的转动惯量系数，其形式为：

，而那些非对角元则称为惯量积：

。对连续体来说，应以体积分代替求和，而质点质量应该为质量密度。因此，如果用

表示坐标轴，则矩阵元

能表示为：

。

在轨道力学计算中，质量通常并不重要，因为物体的运动是由重力决定的。系统的主体通常比周围运动的任何物体都大得多，因此可以忽略较小物体对其的引力影响；实际上，它保持恒定的速度。无论质量如何，所有物体的运动都以相同的方式受到重力的影响，因此在相同的条件下，所有物体的运动方式大致相同。在天体动力学和天体力学中，与角动量密切相关的量被定义为：

，称为比角动量。注意

。

对于粒子系统，总角动量只是各个粒子角动量的总和，并且质心是系统的质心。在笛卡尔坐标系中：

，其中x、y、z分别为粒子相对于原点在x轴、y轴、z轴方向的距离，

、

、

分别为粒子在各个方向上的动量分量，

、

、

分别是笛卡尔坐标系中的三个单位向量，表示各个坐标轴的方向，

用于计算两个向量的叉积。即：

，其中

表示粒子在xy平面上的角动量。角速度也可以定义为反对称二阶张量，其分量为

，表示粒子在i和j方向上的角速度。两个反对称张量之间的关系由转动惯量给出，转动惯量现在必须是一个四阶张量：

，其中

表示粒子在旋转过程中各个方向上的惯性力矩，四个指标i、j、k、l可以取x、y、z，表示粒子上三个相互正交的坐标系，

表示粒子在各个方向上的转动惯量。在相对论力学中，粒子的相对论角动量表示为二阶反对称张量：

，用四个矢量表示，即四个位置的

和四个动量的

，并将上述

与质矩（粒子的相对论质量与其质心的乘积）纳入其中。这样的表示可以被认为是对物体质心运动的描述，因为在广义相对论中，质能是守恒的。

在电磁体系中，电磁场对带电体的作用力为：

，其中

为带电体电荷分布，

为电场，

为磁流密度，

为磁场，

为带电体体积元。故力矩为：

。

牛顿第三运动定律的旋转模拟可以这样写：“在封闭系统中，如果不对其他物质施加绕同一轴的相等且相反的扭矩，则任何物质都不能施加扭矩。” 因此，角动量可以在封闭系统中的物体之间进行交换，但交换前后的总角动量保持不变（守恒）。从另一个角度来看，牛顿xxx运动定律的旋转类比可以写成：“除非受到外部影响，否则刚体将继续处于匀速旋转状态。” 因此，在没有外部影响作用的情况下，系统的原始角动量保持恒定。诺特定理指出，每个守恒定律都与基础物理的对称性（不变量）相关。与角动量守恒相关的对称性是旋转不变性。如果一个系统绕轴旋转任何角度，其物理性质都不会改变，则意味着角动量是守恒的。角动量守恒定律也可以从牛顿第二定律中推导出来。假设某一刚体由大量质点组成，某时刻角速度为

，角加速度为

。现研究质量为

、距转轴垂直距离为

的任意质点k，作用在k上的力可以分为外力

（来自刚体以外一切力的合力）以及内力

（来自刚体以内各质点对质点k作用力的合力），按牛顿第二定律，有：

，

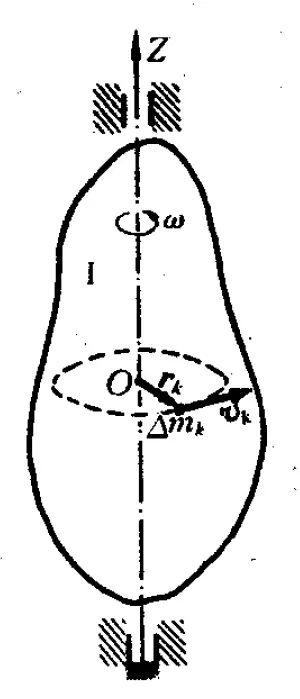刚体绕轴旋转

将两边投影到质点k圆轨迹切线方向，有：

，对两边乘以

，并对整个刚体求和，则有：

，其中等式右边xxx项为合外力矩，第二项为所有内力对旋转轴的力矩总和。由于内力成对出现，而且大小相等、方向相反，因此所有内力对旋转轴的力矩总和恒等于0。

在拉格朗日力学中，围绕给定轴旋转的角动量是围绕同一轴的角度的广义坐标和共轭动量：

，其中

是围绕z轴旋转角度对时间的导数，即角速度

。通常，拉格朗日量可以表示为动能与角速度的函数。对于密度为

非点状物体，在其物体区域上进行积分，有：

。

经典上，一个粒子的轨道角动量（相对于原点）由下式给出：

,其中p是物体的动量。其在各个方向的分量

、

、

分别为，

，其中x、y、z分别为粒子相对于原点在x轴、y轴、z轴方向的距离，

、

、

分别为粒子在各个方向上的动量分量。对应的量子算符由

，

，

得到，其中

为约化普朗克常数，

为虚数。在量子物理学中，还有另一种角动量，称为自旋角动量，用自旋算子

表示。自旋通常被描述为绕轴旋转的粒子，但事实上，自旋是粒子的固有属性，与空间中的任何运动无关，并且与轨道角动量有着根本的不同。所有基本粒子都具有特征自旋（可能为零），并且几乎所有基本粒子都具有非零自旋。对于一个粒子，总角动量

结合了所有粒子和场的自旋角动量和轨道角动量。角动量守恒适用于

，但不适用于

或

。例如，自旋轨道相互作用允许角动量在

和

之间来回转移，而总角动量保持恒定。电子和光子不需要具有基于整数的总角动量值。

动量矩定理给出质点系对矩心点动量矩的变化与外力对该点主矩之间的关系。选固定点O为矩心(取矩中心)，则动量矩定理为:

式中Lo为质点系对点O的动量矩:

为质点系中所有质点所受外力对点O的力矩M_i的总和。质点系动量矩定理表述为:质点系对固定点的动量矩对时间的导数等于外力对该点的主矩。式(1)为微分形式，在某时间间隔 【t1，t2】上积分还可得动量矩定理的积分形式：

当质点系所受外力对某固定点或某固定轴的力矩为零时，相应的动量矩保持不变，是为动量矩守恒情况。