运动规划

运动规划，也称为路径规划是一个计算问题，以找到一个有效的配置序列，将物体从源头移动到目的地。这个术语被用于计算几何学、计算机动画、机器人和计算机游戏。例如，考虑为建筑物内的移动机器人导航，使其到达一个遥远的航点。它应该在执行这项任务的同时避开墙壁，不掉下楼梯。运动规划算法将把这些任务的描述作为输入，并产生发送给机器人车轮的速度和转向命令。运动规划算法可能会解决具有更多关节的机器人、更复杂的任务、不同的约束和不确定性。运动规划在机器人领域有若干应用，如自主性、自动化和CAD软件中的机器人设计，以及在其他领域的应用，如数字人物的动画、视频游戏、建筑设计、机器人手术和生物分子的研究。

一个基本的运动规划问题是计算一条连接起始配置S和目标配置G的连续路径，同时避免与已知障碍物发生碰撞。机器人和障碍物的几何形状在二维或三维工作空间中描述，而运动则表示为配置空间（可能是高维）中的路径。

一个配置描述了机器人的姿势，而配置空间C是所有可能配置的集合。比如说。如果机器人是一个在二维平面（工作空间）中平移的单点（零尺寸），C就是一个平面，一个配置可以用两个参数（x，y）来表示。如果机器人是一个可以平移和旋转的二维形状，工作空间仍然是二维的。

自由空间避免与障碍物碰撞的配置集被称为自由空间Cfree。Cfree在C中的补充被称为障碍物或禁止区域。通常，明确地计算Cfree的形状是非常困难的。然而，测试一个给定的配置是否在Cfree中是有效的。首先，前向运动学确定机器人的几何形状的位置，而碰撞检测则测试机器人的几何形状是否与环境的几何形状发生碰撞。

目标空间是自由空间的一个子空间，表示我们希望机器人移动到哪里。在全局运动规划中，目标空间是可以被机器人的传感器观察到的。然而，在局部运动规划中，机器人在某些状态下无法观察到目标空间。为了解决这个问题，机器人会经过几个虚拟的目标空间，每个目标空间都位于可观察的区域内（机器人周围）。一个虚拟目标空间被称为一个子目标。

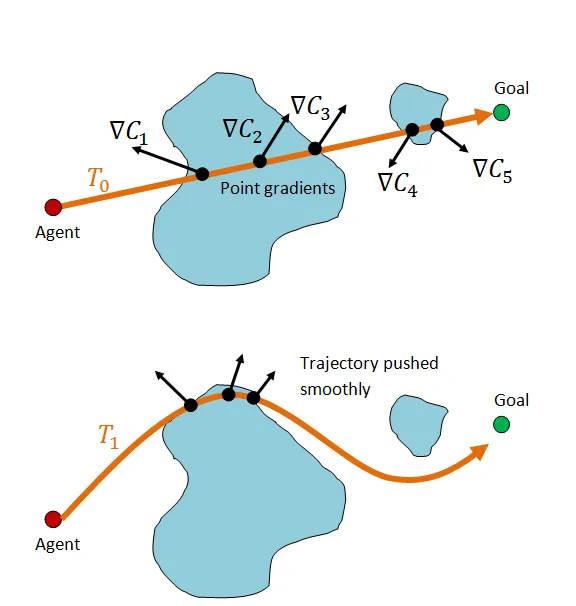
障碍物空间是机器人不能移动的空间。障碍空间与自由空间不相反。

低维问题可以用基于网格的算法来解决，这种算法在配置空间的顶部覆盖一个网格，或者用几何算法来计算Cfree的形状和连接性。复杂约束条件下的高维系统的精确运动规划在计算上是难以实现的。电势场算法是有效的，但会受到局部最小值的影响（谐波电势场是一个例外）。基于抽样的算法避免了局部最小值的问题，并能相当快地解决许多问题。它们不能确定没有路径存在，但它们有一个失败的概率，随着花费的时间越多，概率越小。基于采样的算法目前被认为是在高维空间中进行运动规划的最先进的方法，并已被应用于有几十甚至几百个维度的问题。

基于网格的方法在配置空间上覆盖了一个网格，并假设每个配置都被识别为一个网格点。在每个网格点，只要它们之间的线完全包含在Cfree内，机器人就可以移动到相邻的网格点。